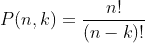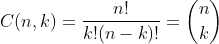Given an integer n, return the number of ways it can be represented as a sum of 1s and 2s

Question

For example:

5 = 1+1+1+1+1

5 = 1+1+1+2

5 = 1+1+2+1

5 = 1+2+1+1

5 = 2+1+1+1


5 = 1+2+2

5 = 2+2+1

5 = 2+1+2

Can anyone give a hint for a pseudo code on how this can be done please. Honestly have no clue how to even start. Also this looks like an exponential problem can it be done in linear time?

Thank you.

Answer 1

In the example you have provided order of addends is important. (See the last two lines in your example). With this in mind, the answer seems to be related to Fibonacci numbers. Let's F(n) be the ways n can be written as 1s and 2s. Then the last addened is either 1 or 2. So F(n) = F(n-1) + F(n-2). These are the initial values:

F(1) = 1 (1 = 1)
F(2) = 2 (2 = 1 + 1, 2 = 2)

Answer 2

This is actually the (n+1)th Fibonacci number. Here's why:

Let's call f(n) the number of ways to represent n. If you have n, then you can represent it as (n-1)+1 or (n-2)+2. Thus the ways to represent it are the number of ways to represent it is f(n-1) + f(n-2). This is the same recurrence as the Fibonacci numbers. Furthermore, we see if n=1 then we have 1 way, and if n=2 then we have 2 ways. Thus the (n+1)th Fibonacci number is your answer. There are algorithms out there to compute enormous Fibonacci numbers very quickly.

Answer 3

Permutations

If we want to know how many possible orderings there are in some set of size n without repetition (i.e., elements selected are removed from the available pool), the factorial of n (or n!) gives the answer:

double factorial(int n)
{
    if (n <= 0)
        return 1;
    else
        return n * factorial(n - 1);
}

Note: This also has an iterative solution and can even be approximated using the gamma function:

std::round(std::tgamma(n + 1)); // where n >= 0

---

The problem set starts with all 1s. Each time the set changes, two 1s are replaced by one 2. We want to find the number of ways k items (the 2s) can be arranged in a set of size n. We can query the number of possible permutations by computing:

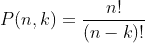
double permutation(int n, int k)
{
    return factorial(n) / factorial(n - k);
}

However, this is not quite the result we want. The problem is, permutations consider ordering, e.g., the sequence 2,2,2 would count as six distinct variations.

Combinations

These are essentially permutations which ignore ordering. Since the order no longer matters, many permutations are redundant. Redundancy per permutation can be found by computing k!. Dividing the number of permutations by this value gives the number of combinations:

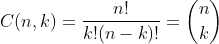
Note: This is known as the binomial coefficient and should be read as "n choose k."

double combination(int n, int k)
{
    return permutation(n, k) / factorial(k);
}

int solve(int n)
{
    double result = 0;

    if (n > 0) {
        for ( int k = 0; k <= n; k += 1, n -= 1 )
            result += combination(n, k);
    }
    return std::round(result);
}

This is a general solution. For example, if the problem were instead to find the number of ways an integer can be represented as a sum of 1s and 3s, we would only need to adjust the decrement of the set size (n-2) at each iteration.

Fibonacci numbers

The reason the solution using Fibonacci numbers works, has to do with their relation to the binomial coefficients. The binomial coefficients can be arranged to form Pascal's triangle, which when stored as a lower-triangular matrix, can be accessed using n and k as row/column indices to locate the element equal to combination(n,k).

The pattern of n and k as they change over the lifetime of solve, plot a diagonal when viewed as coordinates on a 2-D grid. The result of summing values along a diagonal of Pascal's triangle is a Fibonacci number. If the pattern changes (e.g., when finding sums of 1s and 3s), this will no longer be the case and this solution will fail.

Interestingly, Fibonacci numbers can be computed in constant time. Which means we can solve this problem in constant time simply by finding the (n+1)th Fibonacci number.

int fibonacci(int n)
{
    constexpr double SQRT_5 = std::sqrt(5.0);
    constexpr double GOLDEN_RATIO = (SQRT_5 + 1.0) / 2.0;

    return std::round(std::pow(GOLDEN_RATIO, n) / SQRT_5);
}

int solve(int n)
{
    if (n > 0)
        return fibonacci(n + 1);
    return 0;
}

As a final note, the numbers generated by both the factorial and fibonacci functions can be extremely large. Therefore, a large-maths library may be needed if n will be large.

Answer 4

Here is the code using backtracking which solves your problem. At each step, while remembering the numbers used to get the sum so far(using vectors here), first make a copy of them, first subtract 1 from n and add it to the copy then recur with n-1 and the copy of the vector with 1 added to it and print when n==0. then return and repeat the same for 2, which essentially is backtracking.

#include <stdio.h>
#include <vector>
#include <iostream>
using namespace std;
int n;
void print(vector<int> vect){
    cout << n <<" = ";
    for(int i=0;i<vect.size(); ++i){
       if(i>0)
           cout <<"+" <<vect[i];
       else cout << vect[i];
    }
    cout << endl;
}

void gen(int n, vector<int> vect){
   if(!n)
      print(vect);
   else{
      for(int i=1;i<=2;++i){
          if(n-i>=0){
              std::vector<int> vect2(vect);
              vect2.push_back(i);
              gen(n-i,vect2);
          }
      }
   }
}

int main(){
   scanf("%d",&n);
   vector<int> vect;
   gen(n,vect);
}

Answer 5

This problem can be easily visualized as follows:

Consider a frog, that is present in front of a stairway. It needs to reach the n-th stair, but he can only jump 1 or 2 steps on the stairway at a time. Find the number of ways in which he can reach the n-th stair?

Let T(n) denote the number of ways to reach the n-th stair.

So, T(1) = 1 and T(2) = 2(2 one-step jumps or 1 two-step jump, so 2 ways)

In order to reach the n-th stair, we already know the number of ways to reach the (n-1)th stair and the (n-2)th stair.

So, once can simple reach the n-th stair by a 1-step jump from (n-1)th stair or a 2-step jump from (n-2)th step...

Hence, T(n) = T(n-1) + T(n-2)

Hope it helps!!!