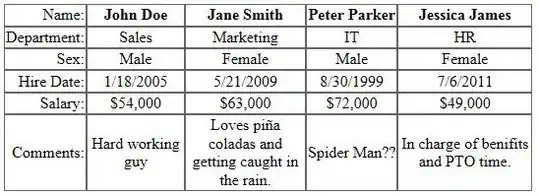
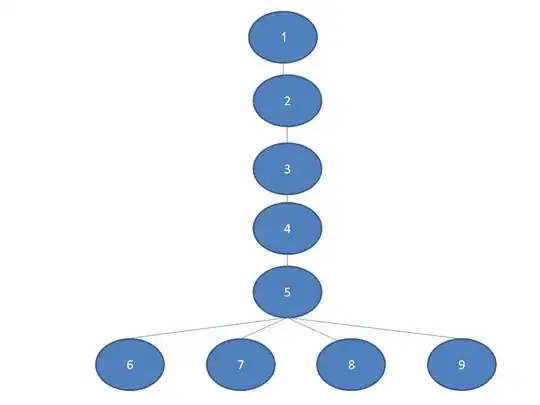
For the algorithm above, I can only figure out the runtime for
if n==0:
is 1 and the runtime for
rec_opt(n-1)
will be T(n-1). But I can't figure out the runtime for
rec_opt(p[n])
and why the recurrence has an exponential closed-form, O(2^n )
And furthermore, why this algorithm will be O(n).