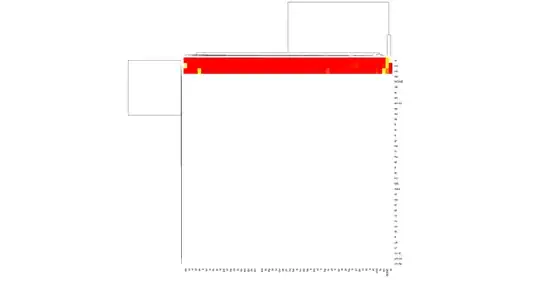
I have implemented ray-tracing of quartic surfaces in GLSL
#version 400 core
in vec2 q; // Screen coordinates. Entire screen is covered by 2 triangles, in which the ray-tracing is done.
uniform vec3 X; // Position of the screen centre in world coordinates.
uniform vec3 R; // View direction in euler angles.
uniform vec2 B; // Screen width and height.
uniform vec3 P; // Position of the eyes in the coordinates given by R.
out vec4 color;
const float pi = 2 * asin (1.0);
// Creating an unit vector from sferical coordinates.
vec3 sfe (const float fi, const float te)
{
return vec3 (cos (fi) * cos (te), sin (fi) * cos (te), sin (te));
}
// Get the vector basis for view space.
mat3 getb (const vec3 r)
{
mat3 M;
M [0] = sfe (r [0], r [1]);
vec3 a = sfe (r [0] + 0.5 * pi, 0);
vec3 b = sfe (r [0], r [1] + 0.5 * pi);
M [1] = a * cos (r [2]) + b * sin (r [2]);
M [2] = - a * sin (r [2]) + b * cos (r [2]);
return M;
}
// Get the pixel position in world coordinates.
vec3 getx (const vec3 e, const vec3 f, const vec2 b, const vec2 q)
{
return b [0] * q [0] * e + b [1] * q [1] * f;
}
// Complex numbers.
// Complex multiplication.
vec2 nb (const vec2 a, const vec2 b)
{
return vec2 (a [0] * b [0] - a [1] * b [1], a [0] * b [1] + a [1] * b
[0]);
}
// Complex conjugate.
vec2 ks (const vec2 z)
{
return vec2 (z [0], - z [1]);
}
// Complex division.
vec2 lm (const vec2 a, const vec2 b)
{
return nb (a, ks (b)) / dot (b, b);
}
// Complex exponential.
vec2 ena (const vec2 z)
{
return exp (z [0]) * vec2 (cos (z [1]), sin (z [1]));
}
// Complex logarithm.
vec2 ln (const vec2 z)
{
float f;
if (z [0] > 0)
f = 0;
else
f = pi;
return vec2 (0.5 * log (dot (z, z)), atan (z [1] / z [0]) + f);
}
// Complex power.
vec2 om (const float n, const vec2 z)
{
if (z == vec2 (0, 0))
return vec2 (0, 0);
else
return ena (n * ln (z));
}
// Ferrari's solution to quartic equation
// Solution to degree 2 equation.
vec2 [2] rov2 (const float a [3])
{
vec2 w [2];
float D = a [1] * a [1] - 4 * a [0] * a [2];
w [0] = (- vec2 (a [1], 0) - om (0.5, vec2 (D, 0))) / (2 * a [0]);
w [1] = (- vec2 (a [1], 0) + om (0.5, vec2 (D, 0))) / (2 * a [0]);
return w;
}
// Solution to degree 3 equation.
vec2 [3] rov3 (const float a [4])
{
vec2 w [3];
float p, q;
p = (3 * a [0] * a [2] - a [1] * a [1]) / (3 * a [0] * a [0]);
q = (2 * a [1] * a [1] * a [1] - 9 * a [0] * a [1] * a [2] + 27 * a [0] * a [0] * a [3]) / (27 * a [0] * a [0] * a [0]);
float A [3] = float [3] (1, q, - p * p * p / 27);
vec2 k [2] = rov2 (A);
vec2 u = om (1.0 / 3, k [0]);
vec2 U;
for (int i = 0; i < 3; i = i + 1)
{
U = nb (u, ena (vec2 (0, i * 2 * pi / 3)));
w [i] = U - p / 3 * lm (vec2 (1, 0), U) - vec2 (a [1], 0) / (3 * a [0]);;
}
return w;
}
// Solution to degree 4 equation.
vec2 [4] rov4 (const float a [5])
{
vec2 w [4];
float p, q, r;
p = (8 * a [2] * a [0] - 3 * a [1] * a [1]) / (8 * a [0] * a [0]);
q = (a [1] * a [1] * a [1] - 4 * a [2] * a [1] * a [0] + 8 * a [3] * a [0] * a [0]) / (8 * a [0] * a [0] * a [0]);
r = (- 3 * a [1] * a [1] * a [1] * a [1] + 256 * a [4] * a [0] * a [0] * a [0] - 64 * a [3] * a [1] * a [0] * a [0] + 16 * a [2] * a [1] * a [1] * a [0]) / (256 * a [0] * a [0] * a [0] * a [0]);
if (q == 0)
{
float A [3] = float [3] (1, p, r);
vec2 k [2] = rov2 (A);
w [0] = om (0.5, k [0]);
w [1] = - om (0.5, k [0]);
w [2] = om (0.5, k [1]);
w [3] = - om (0.5, k [1]);
}
else
{
float B [4] = float [4] (8, 8 * p, 2 * p * p - 8 * r, - q * q);
vec2 m [3] = rov3 (B);
float o2 = sqrt (2.0f);
vec2 omm = om (0.5, m [0]);
vec2 om1 = om (0.5, - (2.0f * vec2 (p, 0) + 2.0f * m [0] - o2 * q * lm (vec2 (1, 0), omm)));
vec2 om2 = om (0.5, - (2.0f * vec2 (p, 0) + 2.0f * m [0] + o2 * q * lm (vec2 (1, 0), omm)));
w [0] = 0.5f * (- o2 * omm - om1) - vec2 (a [1], 0) / (4 * a [0]);
w [1] = 0.5f * (- o2 * omm + om1) - vec2 (a [1], 0) / (4 * a [0]);
w [2] = 0.5f * (+ o2 * omm - om2) - vec2 (a [1], 0) / (4 * a [0]);
w [3] = 0.5f * (+ o2 * omm + om2) - vec2 (a [1], 0) / (4 * a [0]);
}
return w;
}
// Evaluation and derivation of quartic.
struct quartic
{
bool lv [4];
float v4 [15];
float v3 [10];
float v2 [6];
float v1 [3];
float v0;
};
float eval (const quartic q, vec3 v)
{
float x = v [0];
float y = v [1];
float z = v [2];
float S = 0;
if (q.lv [0])
{
S = S + x * x * (x * (q.v4 [0] * x + q.v4 [3] * y + q.v4 [4] * z) + y * (q.v4 [5] * z + q.v4 [12] * y)) +
y * y * (y * (q.v4 [1] * y + q.v4 [6] * z + q.v4 [7] * x) + z * (q.v4 [8] * x + q.v4 [13] * z)) +
z * z * (z * (q.v4 [2] * z + q.v4 [9] * x + q.v4 [10] * y) + x * (q.v4 [11] * y + q.v4 [14] * x));
}
if (q.lv [1])
{
S = S + x * (x * (q.v3 [0] * x + q.v3 [3] * y + q.v3 [4] * z) - q.v3 [9] * y * z) +
y * y * (q.v3 [1] * y + q.v3 [5] * z + q.v3 [6] * x) +
z * z * (q.v3 [2] * z + q.v3 [7] * x + q.v3 [8] * y);
}
if (q.lv [2])
{
S = S + x * (q.v2 [0] * x + q.v2 [3] * y) +
y * (q.v2 [1] * y + q.v2 [4] * z) +
z * (q.v2 [2] * z + q.v2 [5] * x);
}
if (q.lv [3])
S = S + q.v1 [0] * x + q.v1 [1] * y + q.v1 [2] * z;
return S + q.v0;
}
quartic D (const quartic q0, const vec3 v)
{
quartic q;
q.lv = bool [4] (false, false, false, false);
if (q0.lv [0])
{
q.lv [1] = true;
q.v3 = float [10] (4 * q0.v4 [0] * v [0] + q0.v4 [3] * v [1] + q0.v4 [4] * v [2],
q0.v4 [7] * v [0] + 4 * q0.v4 [1] * v [1] + q0.v4 [6] * v [2],
q0.v4 [9] * v [0] + q0.v4 [10] * v [1] + 4 * q0.v4 [2] * v [2],
3 * q0.v4 [3] * v [0] + 2 * q0.v4 [12] * v [1] + q0.v4 [5] * v [2],
3 * q0.v4 [4] * v [0] + q0.v4 [5] * v [1] + 2 * q0.v4 [14] * v [2],
q0.v4 [8] * v [0] + 3 * q0.v4 [6] * v [1] + 2 * q0.v4 [13] * v [2],
2 * q0.v4 [12] * v [0] + 3 * q0.v4 [7] * v [1] + q0.v4 [8] * v [2],
2 * q0.v4 [14] * v [0] + q0.v4 [11] * v [1] + 3 * q0.v4 [9] * v [2],
q0.v4 [11] * v [0] + 2 * q0.v4 [13] * v [1] + 3 * q0.v4 [10] * v [2],
2 * q0.v4 [5] * v [0] + 2 * q0.v4 [8] * v [1] + 2 * q0.v4 [11] * v [2]);
}
if (q0.lv [1])
{
q.lv [2] = true;
q.v2 = float [6] (3 * q0.v3 [0] * v [0] + q0.v3 [3] * v [1] + q0.v3 [4] * v [2],
q0.v3 [6] * v [0] + 3 * q0.v3 [1] * v [1] + q0.v3 [5] * v [2],
q0.v3 [7] * v [0] + q0.v3 [8] * v [1] + 3 * q0.v3 [2] * v [2],
2 * q0.v3 [3] * v [0] + 2 * q0.v3 [6] * v [1] + q0.v3 [9] * v [2],
q0.v3 [9] * v [0] + 2 * q0.v3 [5] * v [1] + 2 * q0.v3 [8] * v [2],
2 * q0.v3 [4] * v [0] + q0.v3 [9] * v [1] + 2 * q0.v3 [7] * v[2]);
}
if (q0.lv [2])
{
q.lv [3] = true;
q.v1 = float [3] (2 * q0.v2 [0] * v [0] + q0.v2 [3] * v [1] + q0.v2 [5] * v [2],
q0.v2 [3] * v [0] + 2 * q0.v2 [1] * v [1] + q0.v2 [4] * v [2],
q0.v2 [5] * v [0] + q0.v2 [4] * v [1] + 2 * q0.v2 [2] * v [2]);
}
if (q0.lv [3])
q.v0 = q0.v1 [0] * v [0] + q0.v1 [1] * v [1] + q0.v1 [2] * v [2];
else
q.v0 = 0;
return q;
}
// Intersection with a ray.
struct ptn
{
vec3 x;
int l;
};
ptn pt (const vec3 x, const int l)
{
ptn p;
p.x = x;
p.l = l;
return p;
}
// Using Taylor series at screen point x0, we are trying to find intersection point in the form x0 + t * v.
ptn nika (const quartic q0, const vec3 x0, const vec3 v)
{
float k0 = eval (q0, x0);
quartic q = D (q0, v);
float k1 = eval (q, x0);
q = D (q, v);
float k2 = eval (q, x0);
q = D (q, v);
float k3 = eval (q, x0);
q = D (q, v);
float k4 = eval (q, x0);
vec2 k [4] = rov4 (float [5] (k4 / 24, k3 / 6, 0.5 * k2, k1, k0));
float t = 0;
int l = 0;
for (int i = 0; i < 4; i = i + 1)
{
if (abs (k [i] [1]) < 0.001 && k [i] [0] >= 0)
if (k [i] [0] < t || l == 0)
{
t = k [i] [0];
l = 1;
}
}
return pt (x0 + t * v, l);
}
// Main loop.
void main()
{
mat3 b = getb (R);
vec3 x_ = transpose (b) * vec3 (0, B * q);
vec3 x = X + x_;
vec3 v = x_ - transpose (b) * P;
quartic q;
q.lv = bool [4] (true, false, true, false);
float r = 0.2;
float R = 1.25;
// A torus.
q.v4 = float [15] (1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 2, 2);
q.v3 = float [10] (0, 0, 0, 0, 0, 0, 0, 0, 0, 0);
q.v2 = float [6] (- 2 * (R * R + r * r), - 2 * (R * R + r * r), 2 * (R * R - r * r), 0, 0, 0);
q.v1 = float [3] (0, 0, 0);
q.v0 = (R * R - r * r) * (R * R - r * r);
ptn p = nika (q, x, v);
vec3 svetlo = vec3 (1, 1, 1);
vec3 barva = vec3 (1, 0.5, 0.4);
color = vec4 (p.l * barva * svetlo, 1.0);
}
The algorithm provides mostly accurate results, hovewer, in some areas a visible noise appears.
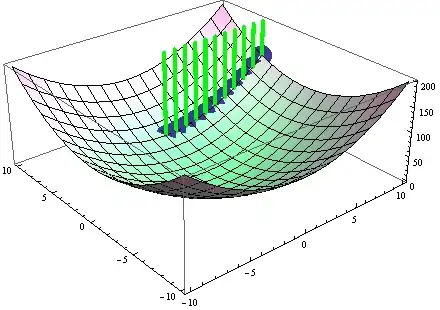
As the quartic (a torus) moves farther away from the screen, noise increases to the point that the torus becomes entirely obscured.
I would like to know the cause of this noise and, if possible, how to eliminate it.
[Edit by Spektre] dictionary
barvameans colorsvetlomeans light