I have been looking for an advanced levenshtein distance algorithm, and the best I have found so far is O(n*m) where n and m are the lengths of the two strings. The reason why the algorithm is at this scale is because of space, not time, with the creation of a matrix of the two strings such as this one:
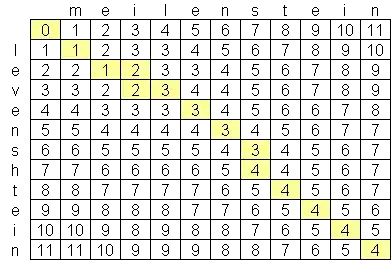
Is there a publicly-available levenshtein algorithm which is better than O(n*m)? I am not averse to looking at advanced computer science papers & research, but haven't been able to find anything. I have found one company, Exorbyte, which supposedly has built a super-advanced and super-fast Levenshtein algorithm but of course that is a trade secret. I am building an iPhone app which I would like to use the Levenshtein distance calculation. There is an objective-c implementation available, but with the limited amount of memory on iPods and iPhones, I'd like to find a better algorithm if possible.