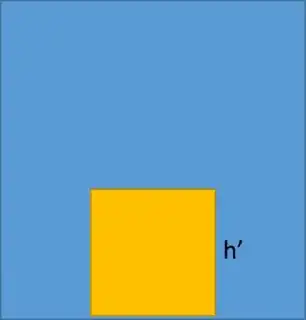
Assuming you know the calibration matrix K, here is a solution that I find simpler than calculating angles. Choose the points p1=(x,y) and p2=(r,s) as indicated in the figure above. Since you say that you know the distance from the camera to the object, that means you know the depth d of these points in camera coordinates, and
Q1=inverse(K)*p1*d
Q2=inverse(K)*p2*d
give you the corresponding points on the cube in camera coordinates. Now the height you seek is simply
abs(Q1-Q2)
Hope that helps.
Edit: Here's a quick explanation about the calibration matrix. When using the pinhole camera model, a 3d point P can be reprojected in the image plane via the multiplication KP where K is (assuming square pixels) the matrix
f 0 a
0 f b
0 0 1
where f is the focal length expressed in terms of pixel size, and [-a,-b]^t is the center of the image coorrdinates system (expressed in pixels). For more info, you can just goolge "intrinsic camera parameters", or for a quick and dirty explanation look here or here. And maybe my other answer can help?
Note: In your case since you only care about depth, you do not need a and b, you can set them to 0 and just set f.
PS: If you don't know f, you should look into camera calibration algorithms (there are auto-calibrating methods but as far as I know they require many frames and fall into the domain of SLAM/SFM). However, I think that you can find pre-computed intrinsic parameters in Blender for a few known smartphone models, but they are not expressed in the exact manner presented above, and you'll need to convert them. I'd calibrate.