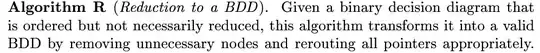How to efficiently implement binary decision diagrams (BDD)?

Question

Background about binary decision diagrams can be found here BDD on wikipedia.

The simplest approach is to build BDT (Binary Decision Tree) and then reduce it due to two rules:
- Merge any isomorphic subgraphs.
- Eliminate any node whose two children are isomorphic.
But there is one major problem BDT can be really huge in comparison to BDD. Is there any way to build BDD without building BDT first?

You never build the unshared decision tree. The BDT is only a way to explain BDDs. — Pascal Cuoq, Nov 02 '10 at 10:46
Since this is about a different meaning of bdd than the bdd tag, I'm going to remove that tag. — Don Roby, Nov 02 '10 at 15:56
A list of existing implementations of binary decision diagrams (~50) in various languages can be found [here](https://github.com/johnyf/tool_lists/blob/master/bdd.md). — 0 _, Mar 02 '15 at 20:52

score 6 · Accepted Answer · answered Nov 02 '10 at 11:13

6

Use the Mk (make node) and Build (construct BDD) algorithms from Andersen, pp. 16-17. I haven't played with BDDs in a while, but I believe either H or T should be a hash table. Use hash tables for both to be on the safe side.

answered Nov 02 '10 at 11:13

Fred Foo

355,277
75
744
836

score 1 · Answer 2 · answered Nov 02 '10 at 15:18

The way to build the BDD is from the parse tree for the expression representing the Boolean function you are trying to build.

I.e., if you want the BDD for (A+B).(C+D), you first parse (A+B).(C+D) into a tree:

   .
  / \
 +   +
/ \ / \
A B C D

then build the BDD recursively - you need methods that can form the AND and the OR of two BDDS, and the base case (single variable BDD).

This works just as well for logic circuits too (view as a parse DAG instead of tree).

These notes on BDDs explain how to implement AND and OR, also the hashtables that are needed to make things work efficiently: http://bit.ly/cuClGe

score 0 · Answer 3 · edited Apr 10 '19 at 15:03

Try to read Knuth, if you want to do it right.

https://www-cs-faculty.stanford.edu/~knuth/fasc1b.ps.gz

To be more precise, the algorithm "R" starting page 14 of that book chapter is a precise and complete answer to the OP;

Overall Knuth's book chapters are a very good in depth reference, it so happens he wrote one on (RO)BDD, which is extremely lucky for anyone seriously trying to implement BDD.

How to efficiently implement binary decision diagrams (BDD)?

3 Answers3