1

I am trying to do non-linear regression using R genetic package (rgp) using technique used here: Fitting a curve to specific data (see second method). I am using R package drc for heartrate data: 

library(drc)

head(heartrate)
#  pressure   rate
#1    50.85 348.76
#2    54.92 344.45
#3    59.23 343.05
#4    61.91 332.92
#5    65.22 315.31
#6    67.79 313.50

library(rgp)

res <- symbolicRegression(rate ~ pressure, data=heartrate)

(symbreg <- res$population[[which.min(sapply(res$population, res$fitnessFunction))]])
#function (pressure) 
#pressure + (pressure/0.853106872646055 + pressure)

ggplot() + 
    geom_point(data=heartrate, aes(pressure,rate), size = 3) +
    geom_line(data=data.frame(symbx=heartrate$pressure, 
                              symby=sapply(heartrate$pressure, symbreg)), 
              aes(symbx, symby), colour = "red")

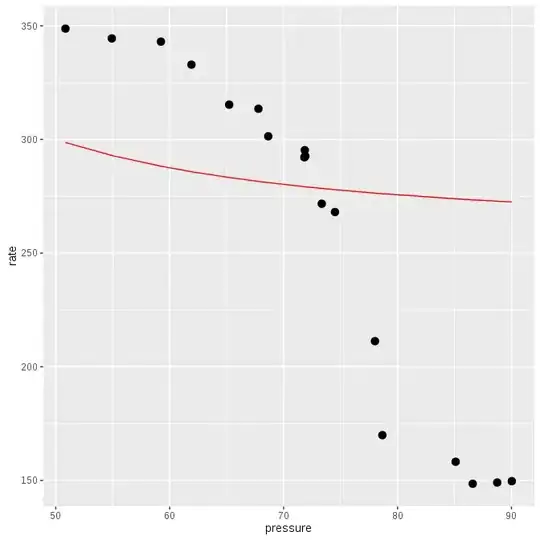
However, the resulting regression line that I am getting is clearly incorrect. The distribution of data points indicate a curvilinear relation with rate reducing as pressure increases (inverse association). However, the regression line generated is linear and in the wrong direction.

enter image description here

Where is the error?

Edit:

Using increased steps as suggested by @cuttlefish44 in comments: 

res = symbolicRegression(rate ~ pressure, data = heartrate, stopCondition = makeStepsStopCondition(45000))

(symbreg <- res$population[[which.min(sapply(res$population, res$fitnessFunction))]])
#function (pressure) 
#exp(exp(exp(cos(cos(-9.23878724686801/pressure)))))

It took 8 minutes to complete. The plot is:

enter image description here

The direction of regression line is better than above (!), but it indicates that it will take a really long time to reach the obvious direction. The regression line with the function obtained by @cuttlefish44 is also similar and not a really good fit.

Community
  • 1
  • 1
rnso
  • 23,686
  • 25
  • 112
  • 234
  • Maybe the default value of `stopCondition`, `makeTimeStopCondition(5)`, is too short in your case ? `symbolicRegression(rate ~ pressure, data = heartrate, stopCondition = makeStepsStopCondition(45000))` gave me `symbreg; function (pressure) exp(exp(exp(exp(tan(6.91310722380877/pressure - sin(0.932394750416279)) * cos(exp(sin(-9.12634917534888)))))))` – cuttlefish44 Dec 04 '16 at 16:07
  • I have added the result with this in question above. – rnso Dec 04 '16 at 16:24

1 Answers1

-1

You may have already read this but I think your answer is hidden somewhere inside this introduction to RGP package written by Oliver Flasch.

I don't know anything about rgppackage but if you only want a linear regression, why don't you use lm()function from the base package ?

At least you would be able to estimate parameters of β0 and β1 for Ordinary least squares regression :

rate = β1*pressure + β0 

     linear.model <- lm(rate ~ pressure, data=heartrate)

     ggplot(data=heartrate, aes(x=pressure,y=rate)) + 
         geom_point() + 
         geom_smooth(method="lm", col="red")

linear regression with ggplot2

You can access the coeficcients with linear.model$coefficients

You can still manipulate the predicted values with linear.model$fitted.values

You have access to the residual with : linear.model$residuals

If you want to fit the curve with more accuracy the linear model might be not sufficient, you can try glm, or a polynomial regression and select the best model with AIC or BIC criteria.

bobolafrite
  • 100
  • 1
  • 11
  • I do not want linear regression and that is exactly why I am using rgp package. I have seen this Introduction to rgp pdf file but there also very similar method is recommended. Why don't you use rgp package and try to get a proper result. – rnso Dec 04 '16 at 13:19
  • Sorry I didn't take a look at your profile you're right, did you see all the warnings indicating you the generation of NAN during the process of symbolicRegression ? – bobolafrite Dec 04 '16 at 13:41
  • That's a really good point. I had not seen warnings() earlier. You should put this in the answer and how to correct this rather than how to do linear regression. – rnso Dec 04 '16 at 13:57
  • I have edited the question to clarify that I am trying to do non-linear regression. – rnso Dec 04 '16 at 16:43