Python: Plotting an Integral

Question

I know there are some similar questions around here but none of them seems to really get to my problem.

My code looks like this:

import numpy 

import matplotlib.pyplot as plt

from scipy import integrate as integrate

def H(z , omega_m , H_0 = 70):

    omega_lambda=1-omega_m
    z_prime=((1+z)**3)
    wurzel=numpy.sqrt(omega_m*z_prime + omega_lambda)

    return H_0*wurzel



def H_inv(z, omega_m , H_0=70):

    return 1/(H(z, omega_m, H_0=70))

def integral(z, omega_m , H_0=70):

    I=integrate.quad(H_inv,0,z,args=(omega_m,))
    return I


def d_L(z, omega_m , H_0=70):

    distance=(2.99*(10**8))*(1+z)*integral(z, omega_m, H_0=70)

    return distance

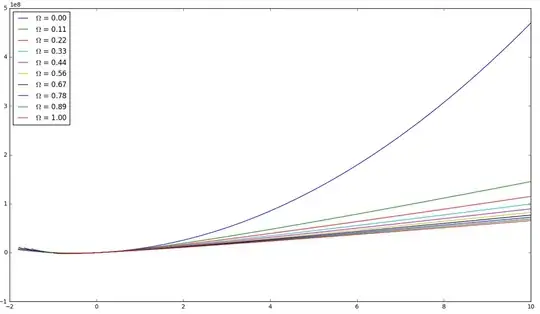
The functions do work, my problem: How can I plot d_L versus z ? Like it's obviously a problem that I have this integral function in the definition of my d_L and it depends on z and some args=(omega_m, ).

Can you give an example of `z`and how you use that in `d_L`? — Julien Marrec, Dec 04 '16 at 17:00
In the end z should run from 0 to 2 with enough steps (500+). — user7248647, Dec 04 '16 at 17:54

score 2 · Accepted Answer · answered Dec 04 '16 at 18:21

To build upon @eyllanesc's solution, here's how you'd plot several values of omega:

import numpy

import matplotlib.pyplot as plt

from scipy import integrate


def H(z, omega_m, H_0=70):
    omega_lambda = 1 - omega_m
    z_prime = ((1 + z) ** 3)
    wurzel = numpy.sqrt(omega_m * z_prime + omega_lambda)

    return H_0 * wurzel


def H_inv(z, omega_m, H_0=70):
    return 1 / (H(z, omega_m, H_0=70))


def integral(z, omega_m, H_0=70):
    I = integrate.quad(H_inv, 0, z, args=(omega_m,))[0]
    return I


def d_L(z, omega_m, H_0=70):
    distance = (2.99 * (10 ** 8)) * (1 + z) * integral(z, omega_m, H_0)
    return distance

z0 = -1.8
zf = 10
zs = numpy.linspace(z0, zf, 1000)

fig, ax = plt.subplots(nrows=1,ncols=1, figsize=(16,9))

for omega_m in np.linspace(0, 1, 10):
    d_Ls = numpy.linspace(z0, zf, 1000)
    for index in range(zs.size):
        d_Ls[index] = d_L(zs[index], omega_m=omega_m)
    ax.plot(zs,d_Ls, label='$\Omega$ = {:.2f}'.format(omega_m))
ax.legend(loc='best')
plt.show()

I really appreciate your effort. This is totally what I wanted! I didn't expect such fast and accurate feedback — user7248647, Dec 04 '16 at 18:31

score 1 · Answer 2 · answered Dec 04 '16 at 17:02

try with my solution:

import numpy

import matplotlib.pyplot as plt

from scipy import integrate


def H(z, omega_m, H_0=70):
    omega_lambda = 1 - omega_m
    z_prime = ((1 + z) ** 3)
    wurzel = numpy.sqrt(omega_m * z_prime + omega_lambda)

    return H_0 * wurzel


def H_inv(z, omega_m, H_0=70):
    return 1 / (H(z, omega_m, H_0=70))


def integral(z, omega_m, H_0=70):
    I = integrate.quad(H_inv, 0, z, args=(omega_m,))[0]
    return I


def d_L(z, omega_m, H_0=70):
    distance = (2.99 * (10 ** 8)) * (1 + z) * integral(z, omega_m, H_0)
    return distance

z0 = -1.8
zf = 10
zs = numpy.linspace(z0, zf, 1000)
d_Ls = numpy.linspace(z0, zf, 1000)
omega_m = 0.2

for index in range(zs.size):
     d_Ls[index] = d_L(zs[index], omega_m=omega_m)
plt.plot(zs,d_Ls)
plt.show()

Output:

Thank you very much, this actually looks like what I want to plot! I will need a few minutes/hours to understand the changes since I am really new to python. What do you think would be a fancy way to plot this into the same figure for different values of omega_m? — user7248647, Dec 04 '16 at 18:01
@user7248647 First, if my answer will help you mark it as correct — eyllanesc, Dec 04 '16 at 18:05

Python: Plotting an Integral

2 Answers2