2

For a project of mine, I am required to do a very fast computation of pow(x,y). Hopefully, it is kinda restricted to a precise domain, but it need to be memory efficient enough too, if it is not fast enough.

Like I said, it is in a short scope of x between 0 and 1, and y between 1 and 2. Therefore, it has to be precise enough on the whole scope to have even a slight diminution when called recursively (and not to stall on a number)

If you guys have run into such a thing or have suggestion...

lmiguelvargasf
  • 63,191
  • 45
  • 217
  • 228
Ludovic Zenohate Lagouardette
  • 187
  • 10
  • 1
    @Mehrdad edited – Ludovic Zenohate Lagouardette Dec 05 '16 at 11:44
  • 1
    In what way is `exp(y*log(x))` too slow? -- What precision do you consider as sufficient? -- Try `x^y = x*(1+(x-1))^(y-1) = x*(1+(y-1)*(x-1)+(y-1)*(y-2)/2*(x-1)^2 + O(x-1)^3` as approximation. – Lutz Lehmann Dec 05 '16 at 11:47
  • Have you considered trying a lookup table? – Vittorio Romeo Dec 05 '16 at 11:48
  • 3
    I would be surprised if one were to come up with something better than the native implementation of `pow()` in the C++ library, which will likely use native FPU instructions to do the calculations. – Sam Varshavchik Dec 05 '16 at 11:54
  • Possible duplicate of http://stackoverflow.com/q/6475373/541686 – user541686 Dec 05 '16 at 11:55
  • 2
    @SamVarshavchik : You will be surprised if you look at the actual source of a libc implementation of pow like http://www.cise.ufl.edu/~cop4600/cgi-bin/lxr/http/source.cgi/lib/math/pow.c or https://github.com/evanphx/ulysses-libc/blob/master/src/math/pow.c . – Lutz Lehmann Dec 05 '16 at 12:04
  • @SamVarshavchik Problem with native pow(x,y) is that it is for y as an integer if I remember well – Ludovic Zenohate Lagouardette Dec 05 '16 at 12:16
  • No, pow(x,y) is for floating point arguments both. Which leads to common questions when people expect it to work like a pure integer version. – Lutz Lehmann Dec 05 '16 at 12:26
  • 1
    @SamVarshavchik : What I meant to say was that it depends on what quality you address with "better". The usual implementation strive for the most exact results, so one can gain some speed by sacrificing some bits of accuracy. – Lutz Lehmann Dec 05 '16 at 12:29

2 Answers2

3

Replace pow(x,y) by 

exp(y*log(x))

This is also sometimes the C library implementation but gives slightly distorted results for many integer inputs. Thus the pow(x,y) implementation usually has an overhead to catch trivial powers with exponents 0 and 1, integer powers, and does some other transformations to get the most precise result. Cutting out this overhead may be already a sufficient speed-up.

Lutz Lehmann
  • 25,219
  • 2
  • 22
  • 51
  • Do you think optimizing log with a lookup table could bring some more benefits since x as a defined range ? BTW thats the kind of answers i wanted – Ludovic Zenohate Lagouardette Dec 05 '16 at 12:19
  • That completely depends on the processor and has to be tested. `exp(y*log(x))` requires to load two arguments on the FPU stack, do two FPU internal operations and store the result. A lookup table requires coordination of FPU, CPU and processor cache, which seems to be more complexity. But this is for standard PC architecture. On microprocessors other limitations may lead to other preferences. – Lutz Lehmann Dec 05 '16 at 12:24
  • In my experience, the replacement suggested here typically increases performance of the exponentiation by a factor of two with modern math libraries (probably less so with old libraries targeting x87 FPUs). – njuffa Dec 05 '16 at 13:42
  • 1
    Don't STD log and exp have overhead too btw ? – Ludovic Zenohate Lagouardette Dec 05 '16 at 18:30
  • One would have to compile a small program to asm to check on this, but I think that if there is a FPU command, it will be used, the only overhead being stack operations and wait cycles. – Lutz Lehmann Dec 05 '16 at 18:49
1

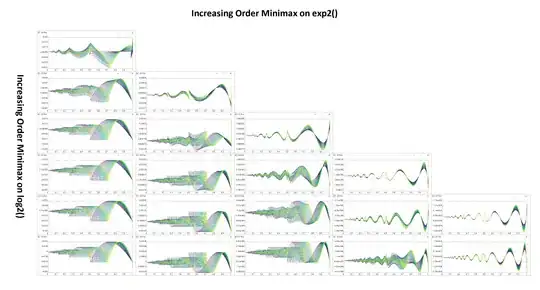
Over such a bounded interval for both x & p the most optimal method is to run two optimized approximations of exp2() and log2(). Since the error from the exp2() minimax polynomial will compound exponentially but the input is always p*log2(x) ≤ 0 for 0 < x ≤ 1 the error will be well behaved. Note: at x = 0, log2(0) = -∞. Below is the sample code for a powf() routine and the error plots of both multiple powers 1 ≤ p ≤ 2 and multiple order minimax approximations for both log2() and exp2 that hopefully satisfy your absolute error tolerance.

image

float aPowf(float x, float p){
    union { float f; uint32_t u; } L2x, e2e;
    float pL2, pL2r, pL2i, E2;

    if(x == 0)  return(0.0f);

    /* Calculate log2(x) Approximation */
    L2x.f = x;
    pL2 = (uint8_t)(L2x.u >> 23) - 127;                 // log2(m*2^e) = log2(m) + e
    L2x.u = (L2x.u & ~(0xFF << 23)) | (0x7F << 23);

    // Approximate log2(x) over 1 <= x < 2, use fma() fused multiply accumulate function for efficient evaluation
    // pL2 += -0xf.4fb9dp-4 + L2x.f;    // 4.303568e-2
    // pL2 += -0x1.acc4cap0 + L2x.f *  (0x2.065084p0 + L2x.f *  (-0x5.847fe8p-4));  // 4.9397e-3
    // pL2 += -0x2.2753ccp0 + L2x.f *  (0x3.0c426p0 + L2x.f *  (-0x1.0d47dap0 + L2x.f *  0x2.88306cp-4));   // 6.3717e-4
    pL2 += -0x2.834a9p0 + L2x.f *  (0x4.11f1d8p0 + L2x.f *  (-0x2.1ee4fcp0 + L2x.f *  (0xa.52841p-4 + L2x.f *  (-0x1.4e4cf6p-4)))); // 8.761e-5
    // pL2 += -0x2.cce408p0 + L2x.f *  (0x5.177808p0 + L2x.f *  (-0x3.8cfd5cp0 + L2x.f *  (0x1.a19084p0 + L2x.f *  (-0x6.aa30dp-4 + L2x.f *  0xb.7cb75p-8))));  // 1.2542058e-5
    // pL2 += -0x3.0a3514p0 + L2x.f *  (0x6.1cbb88p0 + L2x.f *  (-0x5.5737a8p0 + L2x.f *  (0x3.490a04p0 + L2x.f *  (-0x1.442ae8p0 + L2x.f *  (0x4.66497p-4 + L2x.f *  (-0x6.925fe8p-8))))));    // 1.8533e-6
    // pL2 += -0x3.3eb71cp0 + L2x.f *  (0x7.2194ep0 + L2x.f *  (-0x7.7cf968p0 + L2x.f *  (0x5.c642f8p0 + L2x.f *  (-0x2.faeb44p0 + L2x.f *  (0xf.9e012p-4 + L2x.f *  (-0x2.ef86f8p-4 + L2x.f *  0x3.dc524p-8)))))); // 2.831e-7
    // pL2 += -0x3.6c382p0 + L2x.f *  (0x8.23b47p0 + L2x.f *  (-0x9.f803dp0 + L2x.f *  (0x9.3b4f3p0 + L2x.f *  (-0x5.f739ep0 + L2x.f *  (0x2.9cb704p0 + L2x.f *  (-0xb.d395dp-4 + L2x.f *  (0x1.f3e2p-4 + L2x.f *  (-0x2.49964p-8))))))));  // 4.7028674e-8

    pL2 *= p;
//  if(pL2 <= -128)     return(0.0f);

    /* Calculate exp2(p*log2(x)) */
    pL2i = floorf(pL2);
    pL2r = pL2 - pL2i;
    e2e.u = ((int)pL2i + 127) << 23;

    // Approximate exp2(x) over 0 <= x < 1, use fma() fused multiply accumulate function for efficient evaluation.
    // E2 = 0xf.4fb9dp-4 + pL2r;    // 4.303568e-2
    // E2 = 0x1.00a246p0 + pL2r * (0xa.6aafdp-4 + pL2r * 0x5.81078p-4); // 2.4761e-3
    // E2 = 0xf.ff8fcp-4 + pL2r * (0xb.24b0ap-4 + pL2r * (0x3.96e39cp-4 + pL2r * 0x1.446bc8p-4));   // 1.0705e-4
    E2 = 0x1.00003ep0 + pL2r * (0xb.1663cp-4 + pL2r * (0x3.ddbffp-4 + pL2r * (0xd.3b9afp-8 + pL2r * 0x3.81ade8p-8)));   // 3.706393e-6
    // E2 = 0xf.ffffep-4 + pL2r * (0xb.1729bp-4 + pL2r * (0x3.d79b5cp-4 + pL2r * (0xe.4d721p-8 + pL2r * (0x2.49e21p-8 + pL2r * 0x7.c5b598p-12))));  // 1.192e-7
    // E2 = 0x1.p0 + pL2r * (0xb.17215p-4 + pL2r * (0x3.d7fb5p-4 + pL2r * (0xe.34192p-8 + pL2r * (0x2.7a7828p-8 + pL2r * (0x5.15bd08p-12 + pL2r * 0xe.48db2p-16)))));   // 2.9105833e-9
    // E2 = 0x1.p0 + pL2r * (0xb.17218p-4 + pL2r * (0x3.d7f7acp-4 + pL2r * (0xe.35916p-8 + pL2r * (0x2.761acp-8 + pL2r * (0x5.7e9f9p-12 + pL2r * (0x9.70c6ap-16 + pL2r * 0x1.666008p-16))))));  // 8.10693e-11
    // E2 = 0x1.p0 + pL2r * (0xb.17218p-4 + pL2r * (0x3.d7f7b8p-4 + pL2r * (0xe.35874p-8 + pL2r * (0x2.764dccp-8 + pL2r * (0x5.76b95p-12 + pL2r * (0xa.15ca6p-16 + pL2r * (0xf.94e0dp-20 + pL2r * 0x1.cc690cp-20)))))));    // 3.9714478e-11

    return(E2 * e2e.f);
}

Once the appropriate minimax approximation is chosen make sure to implement the horner polynomial evaluation with fused multiply accumulate operations fma() [which are single cycle instruction].

Increasing the accuracy further can be done by introducing a LUT for a type of range reduction for increased accuracy of the logarithm function.

nimig18
  • 797
  • 7
  • 10