2

I am trying to compute the Mahalanobis distance between each observations of a dataset dat, where each row is an observation and each column is a variable. Such distance is defined as:

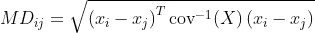
formula

I wrote a function that does it, but I feel like it is slow. Is there any better way to compute this in R ?

To generate some data to test the function:

generateData <- function(nObs, nVar){
  library(MASS)
  mvrnorm(n=nObs, rep(0,nVar), diag(nVar))
  }

This is the function I have written so far. They both work and for my data (800 obs and 90 variables), it takes approximatively 30 and 33 seconds for the method = "forLoop" and method = "apply", respectively.

mhbd_calc2 <- function(dat, method) { #Method is either "forLoop" or "apply"
  dat <- as.matrix(na.omit(dat))
  nObs <- nrow(dat)
  mhbd <- matrix(nrow=nObs,ncol = nObs)
  cv_mat_inv = solve(var(dat))

  distMH = function(x){  #Mahalanobis distance function
    diff = dat[x[1],]-dat[x[2],]
    diff %*% cv_mat_inv %*% diff
  }

  if(method=="forLoop")
  {
    for (i in 1:nObs){
      for(j in 1:i){
        mhbd[i,j] <- distMH(c(i,j))
      }
    }
  }
  if(method=="apply")
  {
    mhbd[lower.tri(mhbd)] = apply(combn(nrow(dat),2),2, distMH)
  }
  result = sqrt(mhbd)
  colnames(result)=rownames(dat)
  rownames(result)=rownames(dat)
  return(as.dist(result))
}

NB: I tried using outer() but it was even slower (60seconds)

Community
  • 1
  • 1
Oligg
  • 375
  • 3
  • 19

1 Answers1

3

You need some mathematical knowledge.

  1. Do a Cholesky factorization of empirical covariance, then standardize your observations;
  2. use dist to compute Euclidean distance on transformed observations.
dist.maha <- function (dat) {
  X <- as.matrix(na.omit(dat))  ## ensure a valid matrix
  V <- cov(X)  ## empirical covariance; positive definite
  L <- t(chol(V))  ## lower triangular factor
  stdX <- t(forwardsolve(L, t(X)))  ## standardization
  dist(stdX)  ## use `dist`
  }

Example

set.seed(0)
x <- matrix(rnorm(6 * 3), 6, 3)

dist.maha(x)
#         1        2        3        4        5
#2 2.362109                                    
#3 1.725084 1.495655                           
#4 2.959946 2.715641 2.690788                  
#5 3.044610 1.218184 1.531026 2.717390         
#6 2.740958 1.694767 2.877993 2.978265 2.794879

The result agrees with your mhbd_calc2.

Zheyuan Li
  • 71,365
  • 17
  • 180
  • 248
  • So, if I understand correctly, you dist.maha is slightly less precise but much faster? With a precision of 7 digits, it is the same with my tests – Oligg Dec 07 '16 at 19:54
  • I might be wrong, but the choleski method doesn't verify if the matrix is nearly singular. If it is the case, it could give high values we don't want, no? Whereas solve() does this verification and returns an error to prevent it. – Oligg Dec 07 '16 at 20:03
  • I think that goes beyond the limit of my knowledge, but I sure will ask around. Also, could you elaborate a little on how your method works if you don't mind? This function will save me big time for sure, thanks alot :) – Oligg Dec 07 '16 at 20:43
  • Hi, I tried to cross validate this solution by using the match_on function in the Optmatch package (the default of which is to calculate pairwise Malahanobis distance) and I am getting different results. Do you have any idea why that might be the case? – Elif Cansu Akoğuz Mar 07 '19 at 15:53