Determine if a point is inside a 4-winged star shape via it's formula extracted from the drawing algorithm

Question

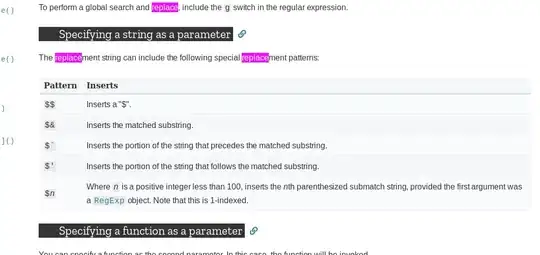
This code draws a star shape :

public void draw(double radius, Color color)
    {
        int x = 0, y = Convert.ToInt32(radius);
        double d = (5 / 4) - radius;
        circlePoint(x, y, color);
        while (x < y)
        {
            if (d < 0)
            {
                d += Math.Pow(x, 2) + 3;
                x++;
                y--;
            }
            else
            {
                d += (x - y) * 2 + 5;
                y--;
            }

            circlePoint(x, y, color);
        }

    }

The drawn shape is shown below

The Actual Question: I want to write a method (bool hasPoint(Point p) ) to check if p is inside this shape. I know for other shapes like a circle or an ellipse, we can check the point's x and y in relative to the object's formula. My Question is "How can I find the formula using the algorithm in draw() ?

Might be helpful: I was messing around with the formula of circle and ellipse and I encountered this shape. It's obvious that it has a relation with those shapes formula.

EDIT:

This is not a polygon. You can see this as a deformed circle (an ellipse actually). In a circle, if p.X-x0^2 + p.Y-y0^2 is less than radius^2, then p is a point inside. You can easily tell that it is the formula of a cirlce: x^2 + y^2 = r^2 .

EDIT 2:

( (x0,y0) is the center point )

void circlePoint(int x, int y, Color foreColor)
    {
        putPixel(x + x0, y + y0);
        putPixel(y + x0, x + y0);
        putPixel(-x + x0, y + y0);
        putPixel(-y + x0, x + y0);
        putPixel(x + x0, -y + y0);
        putPixel(y + x0, -x + y0);
        putPixel(-x + x0, -y + y0);
        putPixel(-y + x0, -x + y0);
    }

void putPixel(int x, int y, Color color){ bitmap.SetPixel(x, y, color); }

EDIT3:

It appears that this curve is mirrored by 8 lines (2 horizontal, 2 vertical and 4 diagonal):

EDIT4:

Based on emrgee's answer I've added these 2 functions, I don't know where I am wrong but it seems hasPointInside() never returns true;

    public double contour(double x)
    {
        double x2 = Math.Pow(x,2);
        return -0.190983 + 0.427051 * Math.Sqrt(0.923607 + (0.647214 * x) - (1.37082 * x2));
    }

    public bool hasPointInside(Point p)
    {

        int min = Math.Min(Math.Abs(p.X), Math.Abs(p.Y));
        int max = Math.Max(Math.Abs(p.X), Math.Abs(p.Y));

        return min <= radius * contour(max / radius);

    }

Answer 1

The draw method computes the star contour iteratively, starting from its tip at (0, radius). For understanding and maintaining the code, as well as for the point-in-star test you need, a closed formula of the contour would be preferable. Trying to extract such a formula from the code, let's first analyze the true branch of the if, which is the only branch taken for the first few iterations. The accumulation of d can be transformed into a closed form for d:

While this already doesn't look like anything related to an ellipse, d gets accumulated with a different formula when in the else branch. I claim it is not possible to transform d into a closed form for the entire algorithm.

Other observations: the slope of the contour can only get -1 or steeper. And there are magic numbers in the formulas not computed from the radius argument. So there are strong indications that the contour resembles an ellipse only accidentally.

Now let's assume you want a star with an ellipsoid contour, with 90° tips and with 90° corners. Let's start with the blue ellipse with major radius 1 in x and minor radius 1/2 in y direction:

We scale and move it so that the green point ends up on the diagonal and the red point, where the slope is -1, ends up at (1,0). With a bit of formula massage, the contour becomes:

or, numerically:

The offset on the x axis is -2 + Sqrt(5) or 0.236068.

Pseudo code for your hasPoint method would then look like this:

with this result for radius 30:

In C#, you would provide these methods:

    /// <summary>
    /// Calculates a contour point of the four-pointed star.
    /// </summary>
    /// <param name="x">The abscissa of the contour point.</param>
    /// <returns>Returns the ordinate of the contour point.</returns>
    private static double StarContour(double x)
    {
        return -0.190983d + (0.427051d * Math.Sqrt(0.923607d + (0.647214d * x) - (1.37082d * x * x)));
    }

    /// <summary>
    /// Tests whether a point is inside the four-pointed star of the given radius.
    /// </summary>
    /// <param name="radius">The radius of the star.</param>
    /// <param name="x">The abscissa of the point to test.</param>
    /// <param name="y">The ordinate of the point to test.</param>
    /// <returns>Returns <see langword="true" /> if the point (<paramref name="x" />, <paramref name="y" />
    /// is inside or on the contour of the star with the given <paramref name="radius" />;
    /// otherwise, if the point is outside the star, returns <see langword="false" />.</returns>
    private static bool InFourStar(double radius, double x, double y)
    {
        double min = Math.Abs(x);
        double max = Math.Abs(y);
        if (min > max)
        {
            // swap min and max
            double h = min;
            min = max;
            max = h;
        }

        return min <= radius * StarContour(max / radius);
    }

and then use them like this:

    /// <summary>
    /// Draws the outline of a four-pointed star of given radius and color.
    /// </summary>
    /// <param name="radius">The radius of the star.</param>
    /// <param name="color">The color of the outline.</param>
    private void DrawFourStar(double radius, Color color)
    {
        const double Offset = 0.236068d;
        for (int x = (int)(Offset * radius); x < radius; ++x)
        {
            int y = (int)(radius * StarContour(x / radius));
            this.CirclePoint(x, y, color);
        }
    }

    /// <summary>
    /// Draws sample points inside or on a four-pointed star contour of given radius.
    /// </summary>
    /// <param name="radius">The radius of the star.</param>
    /// <param name="color">The color of the sample points.</param>
    private void DrawSamplesInStar(double radius, Color color)
    {
        const int SamplingStep = 10;
        for (int x = (int)(-radius); x < radius; x += SamplingStep)
        {
            for (int y = (int)(-radius); y < radius; y += SamplingStep)
            {
                if (InFourStar(radius, x, y))
                {
                    this.bitmap.SetPixel(x + this.x0, y + this.y0, color);
                }
            }
        }
    }

which looks like this for radius 200: