2

How can I prove that n! is not in O(n^p) for any constant natural number p? And is (n k)(n choose k) in O(n^p), for all k?

3 Answers3

10

Stirling's approximation says that

log (n!) = n log n - n + O(log n) = O(n log n)

But

log (n^p) = p log n = O(log n)

for constant p. Clearly n! grows faster than n^p and hence it is not O(n^p).

casablanca
  • 69,683
  • 7
  • 133
  • 150
  • 1
    You could also note without using stirlings approximation that log(n!)=log(n)+log(n-1)+...+log(2)+log(1). log(1)=0, so every other term has to be _at least_ log(2) or larger. That gives log(n!) > n*log(2), which of course means it's O(n). As you noted it's actually O(n*log n), but O(log n) also grows way faster than O(log n). – Emil H Nov 07 '10 at 01:10
  • +1. I was attempting not to do the homework for them ;). but I probably should have hinted at Stirling's factorial approximation. – Mitch Wheat Nov 07 '10 at 01:10
8

You can prove that n! is not in O(n^p) for any constant natural number p, by showing that you can always choose n (for a fixed constant p), so that n! > n^p.

(to get an idea, pick a few low values of p and plot n! against n^p)

The reasoning for the second part follows the same lines. Bound (n choose k) and then use first part.

Hint: as Casablanca noted, you can use Stirling's approximation

Mitch Wheat
  • 295,962
  • 43
  • 465
  • 541
  • 1
    To be precise, *for all* n > n0, where n0 is some positive integer. You can't choose a single value n. Counterexample: p=10, n=2. 2^10 > 2!. – Steve Tjoa Nov 07 '10 at 01:02
  • I'm sorry, I should revise that comment. To *disprove* n! = O(n^p): given p, then for *any* n0 > 0, there exists a (single) value n > n0 such that n! > n^p. – Steve Tjoa Nov 07 '10 at 01:42
2

Edit (3/2011) - easier method using only simple calculus

One way to show O(n!) does not equal O(n^p) is to compare the log of n! with the log of n^p.

ln(n!) = sum(ln(i)) {i: 1 to n}

ln(n^p) = p*ln(n)

That doesn't seem to help since we don't know what the sum of the logs would be. The trick is to calculate a lower bound by using the integral of ln(i)di from 1 to n

This can be seen in the image below that the ln(x) in black is less than the sum step function in blue.

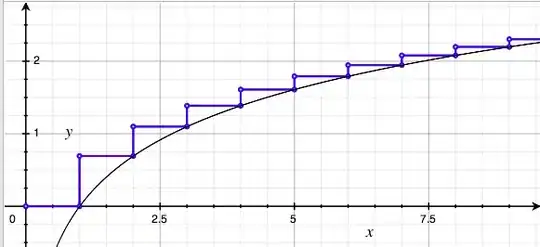
enter image description here

Given that the indefinite integral of ln(i)di is i*ln(i) - i + C, we can integrate from 1 to n to get:

n*ln(n) - n + 1 as the lower bound.

And because no p can be chosen that is larger than all possible n:

O(pln(n)) < O(nln(n)), O(n^p) < O(n!)

note: integrating ln(n) to get an approximation to ln(n!) is the basis for Stirling's approximation. This is a rougher approximation and if you continue it by taking the anti-log: n! >= e*(n/e)^n, whereas Stirling's has sqrt(2*pi*n) instead of e.

Integrating from 1 to n+1 would give you an upper bound (the sum step function would fit inside the graph of ln(n))

Tony Lee
  • 5,622
  • 1
  • 28
  • 45