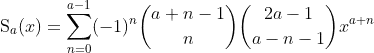General smoothstep equation

Question

I saw this in Wikipedia: Generalization of higher-order equations

My code when I tried to implement it:

function generalSmoothStep(a, x) { //Generalized smoothstep
  var result = 0;
  for (var n = 0; n < a - 1; n ++) {
    result += binom(-a, n) * binom(2 * a - 1, a - n - 1) * Math.pow(x, a + n);
  }
  return result;
}

function smoothStep(x) { //Normal smoothstep
  return -2 * Math.pow(x, 3) + 3 * Math.pow(x, 2);
  //I know about x * x * (3 - 2 * x);
}

function binom(a, b) { //Binomial coefficient
  return Math.factorial(a) / (Math.factorial(a-b) *  Math.factorial(b));
}

Math.factorial = function(value) { //Factorial
  var result = 1;
  if (value > 0) {
    for (var count = 1; count <= value; count ++) {
      result *= count;
    }
  } else if (value < 0) {
    for (var count = -1; count >= value; count --) {
      result *= count;
    }
  } else {
    result = 1;
  }
  return result;
};

document.getElementById("normalStep").innerHTML = "smoothStep(0.2) = " + smoothStep(0.2);
document.getElementById("generalStep").innerHTML = "generalSmoothStep(2, 0.2) = " + generalSmoothStep(2, 0.2);

<head>
  <script src="https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.0/MathJax.js?config=TeX-MML-AM_CHTML"></script>
  <script>
    MathJax.Hub.Config({
      tex2jax: {inlineMath: [['$','$'], ['\\(','\\)']]}
    });
  </script>
</head>

<body>
  <p>The function: $\operatorname{S}_a(x) = \sum_{n=0}^{a-1} \binom{-a}{n}\binom{2a - 1}{a - n - 1}x^{a + n}$</p>
  
  <p>Here is the result when I run:</p>
  
  <p id="normalStep"></p>
  <p id="generalStep"></p>
</body>

I know about binomial coefficient and factorial, but one problem is factorial can't use with negative number, so I tried to use tricks to bypass it, and failed...

And also the part with ()() chained together, I think it is multiplication ()*() between binom, and multiply with x^(a+n), as above, but it still not work.

Used google with words like: "general smooth step", "smooth step sum" but still not return any good explanation about it...

Anyone have any idea why my code not work, and also how to implement general smoothStep function in Javascript

Note from the future: cdn.mathjax.org is nearing its end-of-life, check https://www.mathjax.org/cdn-shutting-down/ for migration tips. — Peter Krautzberger, Apr 11 '17 at 15:33

score 3 · Accepted Answer · edited Dec 17 '16 at 19:10

You can use Pascal Triangle instead of binomial coefficient to solve the issue. Here is the link for more detail of Pascal Triangle.

https://trans4mind.com/personal_development/mathematics/series/pascalsTriangle.htm https://trans4mind.com/personal_development/mathematics/series/pascalGenCoefficients.gif

Here is the solution using Pascal Triangle.

function generalSmoothStep(a, x) { //Generalized smoothstep
  var result = 0;
  for (var n = 0; n <= a - 1; n++) {
    result += (pascalTriangle(-a, n) * pascalTriangle(2 * a - 1, a - n - 1) * Math.pow(x, a + n));
  }
  return result;
}

function pascalTriangle(a, b){
  var result = 1; 
  for(var i = 1; i <= b; i++){
    result *= ((a - (i - 1)) / i);
  }
  return result;
}

function smoothStep(x) { //Normal smoothstep
  return -2 * Math.pow(x, 3) + 3 * Math.pow(x, 2);
}

console.log("smoothStep(0.3) = " + smoothStep(0.3));
console.log("generalSmoothStep(2, 0.3) = " + generalSmoothStep(2, 0.3));

score 0 · Answer 2 · edited Feb 09 '17 at 15:11

You can replace the negative binomial coefficient with a variant that uses positive numbers. Based on the generalization of negative binomial coefficients as described on another Wikipedia article, the smoothstep equation using positive binomial coefficients would be:

Smoothstep using Positive Polynomials

So the resulting code would be:

function generalSmoothStep(a, x) { //Generalized smoothstep
  var result = 0;
  for (var n = 0; n <= a - 1; n ++) {
    // Change negative binom coeff to positive equivalent
    result += Math.pow(-1, n) * binom(a + n - 1, n) * binom(2 * a - 1, a - n - 1) * Math.pow(x, a + n);
  }
  return result;
}

function binom(a, b) { //Binomial coefficient
  return Math.factorial(a) / (Math.factorial(a-b) *  Math.factorial(b));
}

Math.factorial = function(value) { //Factorial
  var result = 1;
  if (value > 0) {
    for (var count = 1; count <= value; count ++) {
      result *= count;
    }
  } else if (value < 0) {
    for (var count = -1; count >= value; count --) {
      result *= count;
    }
  } else {
    result = 1;
  }
  return result;
}

function smoothStep(x) { //Normal smoothstep
  return -2 * Math.pow(x, 3) + 3 * Math.pow(x, 2);
}

console.log("smoothStep(0.3) = " + smoothStep(0.3));
console.log("generalSmoothStep(2, 0.3) = " + generalSmoothStep(2, 0.3));

However, since this version computes factorials, this function will begin to become less accurate a lot quicker than the code in Tushar Ghosh's answer for larger values of a.

General smoothstep equation

2 Answers2