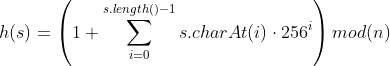Modulo of high powers without using Math.BigInteger

Question

I have to turn this formula into java code:

It would be much easier if I could use libraries such as Math.BigInteger but unfortunately I should do this without it. Some similar question on stackoverflow suggested to write an own bignum library but I want to do it without it.

Right now, my progress is at this step:

int h(String s) {
  long value = 1;
  int mod = ht.length;

  for (int i=0; i < s.length()-1; i++) {
     h += s.charAt(i) * Math.pow(256,i);
  }
  return (int) h % mod;
}

I know that the values of the power gets pretty quick out of the integer range so I thought about writing an own method which calculates the power and modulo of the value. My mathematical knowledge just isn't good enough to know when to use the modulo and how to easy things up.

Thanks in advance!

Answer 1

If you go from the back, you don't have to take any powers at all. Simply multiplying by 256 at each step will have the same effect (values from the back "accumulate" more multiplications, raising them to the required powers). Eg (not tested)

int h(String s) {
  int res = 0;
  int n = ht.length;

  for (int i = s.length() - 1; i >= 0; i--) {
     // using a long here to prevent premature wrapping
     long t = res * 256L + s.charAt(i);
     res = (int)(t % n);
  }
  return (res + 1) % n;
}

Also note that ht.length should not be a power of two (so you can't skip the modulo reduction in the loop, which you could if ht.length was a power of two), because if it's a power of two then the hash depends on (at most) the first 4 characters, which is obviously bad.

Answer 2

I've chosen a large prime for your n by default, ask your tutor, but there's no way it's a good idea to use any non-prime. If that's the number of buckets in a hash table, make sure that number is a prime. Also you mustn't -1 in your for loop's exit condition, you're missing the last character.

private static int MAX_PRIME = 2147483647; //largest positive 32 signed int prime (also happens to be the largest positive 32 signed int)

public static int hash(String s) {
    return hash(s, MAX_PRIME);
}

public static int hash(String s, int primeN) {
    long h = 1;
    long m = 1;

    for (int i = 0; i < s.length(); i++) {
        h += s.charAt(i) * m;
        h %= primeN;
        m *= 256;
        m %= primeN;
    }

    return (int) h;
}

If you want to test the correctness, then you can compare the generated hashes to a BigInteger implementation:

public static int hashBigInt(String s) {
    return hashBigInt(s, MAX_PRIME);
}

public static int hashBigInt(String s, int primeN) {
    final BigInteger bi256 = BigInteger.valueOf(256);
    BigInteger h = BigInteger.ONE;
    BigInteger m = BigInteger.ONE;

    for (int i = 0; i < s.length(); i++) {
        h = h.add(BigInteger.valueOf(s.charAt(i)).multiply(m));
        m = m.multiply(bi256);
    }

    return h.mod(BigInteger.valueOf(primeN))
            .intValue();
}

Answer 3

You should basically move the modulo deeper into the equation to keep the values low at every step. For that you can basically make use of the module rules:

• (a + b) % n = (a % n + b % n) % n
• (a * b) % n = (a % n * b % n) % n

First move it into the loop:

h = (h + s.charAt(i) * Math.pow(256, i)) % mod;

Then move it into the pow as well:

h = (h + s.charAt(i) * Math.pow(256 % mod, i)) % mod;

Finally I would stop using pow and so some custom powering where you mod after each step like
((((256 % mod) * 256 % mod) * 256 % mod) ... )

Answer 4

I think you are looking at Fast modular exponentiation:

Let's consider this simple formula to explain how it works:

x = A^B % C as x = 5^117 % 19

1. Decomposing B into power of two

117 = (2^0 + 2^2 + 2^4 + 2^5 + 2^6) 117 = (1 + 4 + 16 + 32 + 64 )

2. Compute mod C for power of two <= B

5^2 mod 19 = (5^1 * 5^1) mod 19 = (5^1 mod 19 * 5^1 mod 19) mod 19
5^2 mod 19 = (5 * 5) mod 19 = 25 mod 19
5^2 mod 19 = 6

5^4 mod 19 = (5^2 * 5^2) mod 19 = (5^2 mod 19 * 5^2 mod 19) mod 19
5^4 mod 19 = (6 * 6) mod 19 = 36 mod 19
5^4 mod 19 = 17

5^8 mod 19 = (5^4 * 5^4) mod 19 = (5^4 mod 19 * 5^4 mod 19) mod 19
5^8 mod 19 = (17 * 17) mod 19 = 289 mod 19
5^8 mod 19 = 4

5^16 mod 19 = (5^8 * 5^8) mod 19 = (5^8 mod 19 * 5^8 mod 19) mod 19
5^16 mod 19 = (4 * 4) mod 19 = 16 mod 19
5^16 mod 19 = 16

5^32 mod 19 = (5^16 * 5^16) mod 19 = (5^16 mod 19 * 5^16 mod 19) mod 19
5^32 mod 19 = (16 * 16) mod 19 = 256 mod 19
5^32 mod 19 = 9

5^64 mod 19 = (5^32 * 5^32) mod 19 = (5^32 mod 19 * 5^32 mod 19) mod 19
5^64 mod 19 = (9 * 9) mod 19 = 81 mod 19
5^64 mod 19 = 5

3. Compute X

5^117 mod 19 = ( 5^1 * 5^4 * 5^16 * 5^32 * 5^64) mod 19
5^117 mod 19 = ( 5^1 mod 19 * 5^4 mod 19 * 5^16 mod 19 * 5^32 mod 19 * 5^64 mod 19) mod 19
5^117 mod 19 = ( 5 * 17 * 16 * 9 * 5 ) mod 19
5^117 mod 19 = 61200 mod 19 = 1
5^117 mod 19 = 1

Why does this solves your problem

You might have a A or a B which is way above the Integer limit.

Instead of summing ALL the value, and then finaly apply the modulus you can sum up to interger limit and then apply the above formula, then start again summing, and reapply formula, and so on, because 6 % 4 == (3 % 4) + (3 % 4) % 4