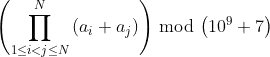Alternate way to compute product of pairwise sums mod 10^9+7 faster than O(N^2)

Question

Given an array A of integers of size N, I want to compute

This was a problem in a past inter-college programming competition. We had to write a program that would solve up to 5 instance of this problem, with N ≤ 200,000 and each a_i ≤ 200,000, within a 20-second run-time limit. Clearly, an O(N²) solution would go over the time limit. According to the editorial, the intended solution involved polynomial multiplication using a fast Fourier transform. I'm looking for alternative algorithms that would solve this faster than the naive O(N²) algorithm without FFT (nor NTT). Are there any simple and elegant solutions to this problem?

Known facts:

mod could be 'distributed' inside the product because (x*y) % m = ((x%m) * (y%m)) % m

Update: here is the input/output testcase file during the contest: if it passes this in 20 seconds, it will be accepted. Input: https://www.dropbox.com/s/nw81hts9rniter5/algol.in?dl=0 Output: https://www.dropbox.com/s/kpa7wit35xr4xm4/algol.out?dl=0

Answer 1

Had give it some more taught and Pascal's triangle is a no go because it would lead to even more operations. Luckily the mod operation can be moved under the PI so you do not need to use big int's but 64 bit arithmetics instead (or 32bit modmul).

PI(ai+aj) mod p == PI((ai+aj)mod p) mod p ... 1<=i<j<=n

so naive C++ solution is (where p<2^16) your task require 64 bit variables instead (which I have no access to in simple therms).

DWORD modpi(DWORD *a,int n,DWORD p)
    {
    int i,j;
    DWORD x=1;
    for (i=0;i<n;i++)
     for (j=i+1;j<n;j++)
        {
        x*=a[i]+a[j];
        x%=p;
        }
    return x;
    }

Now the p is much bigger then max(a[i]) so you could change:

x%=p;

with:

while (x>=p) x-=p;

but on nowadays CPU's is this even slower.

Still this approach is way too slow (~280 ms for n=10000). If we reorder the values (sort them) then suddenly the things got much better. Each value that is in the array multiple times lead to simplification as its partial sum is almost the same. For example:

a[] = { 2,3,3,4 }
x = (2+3).(2+3).(2+4)
  . (3+3).(3+4)
  . (3+4)

the therms for 3 is almost the same so we can use that. count how many of the same a[i] is there then count the partial PI for single of them. power this by the count and for each instance multiply also by a[i]^instance here C++ example:

DWORD modpi1(DWORD *a,int n,DWORD p)
    {
    int i,j,k;
    DWORD x,y,z;
    sort_asc(a,n);
    for (x=1,i=0;i<n;i++)
        {
        // count the values in k
        for (k=1;(i+1<n)&&(a[i]==a[i+1]);i++,k++);
        // compute partial modPI y
        for (y=1,j=i+1;j<n;j++)
            {
            y*=a[i]+a[j];
            y%=p;
            }
        // add the partial modPI y^k;
        for (j=0;j<k;j++)
            {
            x*=y;
            x%=p;
            }
        // add powers for instances of a[i]
        for (k--;k;k--)
         for (j=0;j<k;j++)
            {
            x*=a[i]+a[i];
            x%=p;
            }
        }
    return x;
    }

This gives you some speedup for each multiple occurrence of value in array. But as your array is as big as the possible numbers in it then do not expect too much of this. For uniformly random data where max(a[i])~=n and quick sort is the speed little bit less the 50%. But if you use prime decomposition like MSalters answer suggests you might get a real speedup because then the repetition rate should be much much higher then ~1 but that would need a lot of work handling the equations.

This code is O(N.N') where N' is count of distinct values in a[]. You can also enhance this further to O(N'.N') by:

1. sort a[i] by bucket sort O(n) or quick sort O(n.log(n))

2. do RLE (run length encoding) O(n)

3. account counts also to partial sum O(n'.n') where n'<=n

   The prime decomposition should just change n'<= n to n' <<< n.

Here some measurements using quick sort full 32bit modmul (using 32bit x86 asm which slows things down considerably on my compiler). Random data where max(a[i])~=n:

n=1000;
[   4.789 ms]0: 234954047
[   3.044 ms]1: 234954047
n=10000;
[ 510.544 ms]0: 629694784
[ 330.876 ms]1: 629694784
n=20000;
[2126.041 ms]0: 80700577
[1350.966 ms]1: 80700577

In brackets is the time in [ms], 0: means naive approach, 1: means sorted and partial RLE decompostion of PI. The last value is the result for p=1000000009

If that is still not enough then Apart using DFT/NTT I see no other speedup possible.

[Edit1] full RLE decomposition of a[i]

//---------------------------------------------------------------------------
const DWORD p=1000000009;
const int n=10000;
const int m=n;
DWORD a[n];
//---------------------------------------------------------------------------
DWORD modmul(DWORD a,DWORD b,DWORD p)
    {
    DWORD _a,_b;
    _a=a;
    _b=b;
    asm {
        mov    eax,_a
        mov    ebx,_b
        mul    ebx   // H(edx),L(eax) = eax * ebx
        mov    ebx,p
        div    ebx   // eax = H(edx),L(eax) / ebx
        mov    _a,edx// edx = H(edx),L(eax) % ebx
        }
    return _a;
    }
//---------------------------------------------------------------------------
DWORD modpow(DWORD a,DWORD b,DWORD p)
    {   // b is not mod(p) !
    int i;
    DWORD d=1;
    for (i=0;i<32;i++)
        {
        d=modmul(d,d,p);
        if (DWORD(b&0x80000000)) d=modmul(d,a,p);
        b<<=1;
        }
    return d;
    }
//---------------------------------------------------------------------------
DWORD modpi(DWORD *a,int n,DWORD p)
    {
    int i,j,k;
    DWORD x,y;
    DWORD *value=new DWORD[n+1];// RLE value
    int   *count=new int[n+1];  // RLE count
    // O(n) bucket sort a[] -> count[] because max(a[i])<=n
    for (i=0;i<=n;i++) count[i]=0;
    for (i=0;i< n;i++) count[a[i]]++;
    // O(n) RLE packing value[n],count[n]
    for (i=0,j=0;i<=n;i++)
     if (count[i])
        {
        value[j]=    i;
        count[j]=count[i];
        j++;
        } n=j;
    // compute the whole PI to x
    for (x=1,i=0;i<n;i++)
        {
        // compute partial modPI value[i]+value[j] to y
        for (y=1,j=i+1;j<n;j++)
         for (k=0;k<count[j];k++)
          y=modmul(y,value[i]+value[j],p);
        // add the partial modPI y^count[j];
        x=modmul(x,modpow(y,count[i],p),p);
        // add powers for instances of value[i]
        for (j=0,k=1;k<count[i];k++) j+=k;
        x=modmul(x,modpow(value[i]+value[i],j,p),p);
        }
    delete[] value;
    delete[] count;
    return x;
    }
//---------------------------------------------------------------------------

This is even bit faster as it does sort in O(n) and RLE in O(n) so this is resulting in O(N'.N'). You can take advantage of more advanced modmul,modpow routines if you got any. But for uniform distribution of values is this still no way near usable speeds.

[edit2] full RLE decomposition of a[i]+a[j]

DWORD modpi(DWORD *a,int n,DWORD p) // full RLE(a[i]+a[j]) O(n'.n') n' <= 2n
    {
    int i,j;
    DWORD x,y;
    DWORD nn=(n+1)*2;
    int   *count=new int[nn+1]; // RLE count
    // O(n^2) bucket sort a[] -> count[] because max(a[i]+a[j])<=nn
    for (i=0;i<=nn;i++) count[i]=0;
    for (i=0;i<n;i++)
     for (j=i+1;j<n;j++)
      count[a[i]+a[j]]++;
    // O(n') compute the whole PI to x
    for (x=1,y=0;y<=nn;y++)
     if (count[y])
      x=modmul(x,modpow(y,count[y],p),p);
    delete[] count;
    return x;
    }
//---------------------------------------------------------------------------

And this is even faster nearing desirable times but still few magnitudes off.

n=20000
[3129.710 ms]0: 675975480 // O(n^2) naive
[2094.998 ms]1: 675975480 // O(n'.n) partial RLE decomposition of a[i] , n'<= n
[2006.689 ms]2: 675975480 // O(n'.n') full RLE decomposition of a[i] , n'<= n
[ 729.983 ms]3: 675975480 // T(c0.n^2+c1.n') full RLE decomposition of a[i]+a[j] , n'<= 2n , c0 <<< c1

[Edit3] full RLE(a[i]) -> RLE(a[i]+a[j]) decomposition

I combined all the approaches above and create much faster version. The algrithm is like this:

1. RLE encode a[i]

   simply create a histogram of a[i] by bucket sort in O(n) and then pack to coding value[n'],count[n'] so no zero's are present in the array. This is pretty fast.

2. convert RLE(a[i]) to RLE(a[i]+a[j])

   simply create count of each a[i]+a[j] therm in the final PI similar to RLE(a[i]+a[j]) decomposition but in O(n'.n') without any time demanding operation. Yes this is quadratic but on n'<=n and with very small constant time. But this part is the bottleneck ...

3. compute the modpi from RLE(a[i]+a[j])

   This is simple modmul/modpow in O(n') biggest constant time but low complexity so still very fast.

The C++ code for this:

DWORD modpi(DWORD *a,int n,DWORD p) // T(c0.n+c1.n'.n'+c2.n'') full RLE(a[i]->a[i]+a[j]) n' <= n , n'' <= 2n , c0 <<< c1 << c2
    {
    int i,j,k;
    DWORD x,y;
    DWORD nn=(n+1)*2;
    DWORD *rle_iv =new DWORD[ n+1]; // RLE a[i] value
    int   *rle_in =new int[ n+1];   // RLE a[i] count
    int   *rle_ij=new int[nn+1];    // RLE (a[i]+a[j]) count
    // O(n) bucket sort a[] -> rle_i[] because max(a[i])<=n
    for (i=0;i<=n;i++) rle_in[i]=0;
    for (i=0;i<n;i++)  rle_in[a[i]]++;
    for (x=0,i=0;x<=n;x++)
     if (rle_in[x])
        {
        rle_iv[i]=       x;
        rle_in[i]=rle_in[x];
        i++;
        } n=i;
    // O(n'.n') convert rle_iv[]/in[] to rle_ij[]
    for (i=0;i<=nn;i++) rle_ij[i]=0;
    for (i=0;i<n;i++)
        {
        rle_ij[rle_iv[i]+rle_iv[i]]+=(rle_in[i]*(rle_in[i]-1))>>1; // 1+2+3+...+(rle_iv[i]-1)
        for (j=i+1;j<n;j++)
         rle_ij[rle_iv[i]+rle_iv[j]]+=rle_in[i]*rle_in[j];
        }
    // O(n') compute the whole PI to x
    for (x=1,y=0;y<=nn;y++)
     if (rle_ij[y])
      x=modmul(x,modpow(y,rle_ij[y],p),p);
    delete[] rle_iv;
    delete[] rle_in;
    delete[] rle_ij;
    return x;
    }

And comparison measurements:

n=10000
[ 751.606 ms] 814157062 O(n^2) naive
[ 515.944 ms] 814157062 O(n'.n) partial RLE(a[i]) n' <= n
[ 498.840 ms] 814157062 O(n'.n') full RLE(a[i]) n' <= n
[ 179.896 ms] 814157062 T(c0.n^2+c1.n') full RLE(a[i]+a[j]) n' <= 2n , c0 <<< c1
[  66.695 ms] 814157062 T(c0.n+c1.n'.n'+c2.n'') full RLE(a[i]->a[i]+a[j]) n' <= n , n'' <= 2n , c0 <<< c1 << c2
n=20000
[ 785.177 ms] 476588184 T(c0.n^2+c1.n') full RLE(a[i]+a[j]) n' <= 2n , c0 <<< c1
[ 255.503 ms] 476588184 T(c0.n+c1.n'.n'+c2.n'') full RLE(a[i]->a[i]+a[j]) n' <= n , n'' <= 2n , c0 <<< c1 << c2
n=100000
[6158.516 ms] 780587335 T(c0.n+c1.n'.n'+c2.n'') full RLE(a[i]->a[i]+a[j]) n' <= n , n'' <= 2n , c0 <<< c1 << c2

last times are for this method. Doubling n multiplies the runtime by cca 4 times. so for n=200000 the runtime is around 24 sec on my setup.

[Edit4] my NTT approach for comparison

I know you want to avoid FFT but still I think this is good for comparison. The 32bit NTT is OK for this. Because it is applied only on the histogram which consist only from exponents which are just few bits wide and mostly equal to 1 which prevents overflows even on n=200000. Here C++ source:

DWORD modpi(DWORD *a,int n,int m,DWORD p) // O(n.log(n) RLE(a[i])+NTT convolution
    {
    int i,z;
    DWORD x,y;
    for (i=1;i<=m;i<<=1); m=i<<1;   // m power of 2 > 2*(n+1)
    #ifdef _static_arrays
    m=2*M;
    DWORD rle[2*M];                 // RLE a[i]
    DWORD con[2*M];                 // convolution c[i]
    DWORD tmp[2*M];                 // temp
    #else
    DWORD *rle =new DWORD[m];       // RLE a[i]
    DWORD *con =new DWORD[m];       // convolution c[i]
    DWORD *tmp =new DWORD[m];       // temp
    #endif
    fourier_NTT ntt;
    // O(n) bucket sort a[] -> rle[] because max(a[i])<=n
    for (i=0;i<m;i++) rle[i]=0.0;
    for (i=0;i<n;i++) rle[a[i]]++;

    // O(m.log(m)) NTT convolution
    for (i=0;i<m;i++) con[i]=rle[i];
    ntt.NTT(tmp,con,m);
    for (i=0;i<m;i++) tmp[i]=ntt.modmul(tmp[i],tmp[i]);
    ntt.iNTT(con,tmp,m);
    // O(n') compute the whole PI to x
    for (x=1,i=0;i<m;i++)
        {
        z=con[i];
        if (int(i&1)==0) z-=int(rle[(i+1)>>1]);
        z>>=1; y=i;
        if ((y)&&(z)) x=modmul(x,modpow(y,z,p),p);
        }
    #ifdef _static_arrays
    #else
    delete[] rle;
    delete[] con;
    delete[] tmp;
    #endif
    return x;
    }

You can ignore the _static_arrays (handle it as it is not defined) it is just for simpler debugging. Beware the convolution ntt.modmul is not working with the tasks p but with NTTs modulo instead !!! If you want to be absolutely sure this would work on higher n or different data distributions use 64bit NTT.

Here comaprison to the Edit3 approach:

n=200000
[24527.645 ms] 863132560 O(m^2) RLE(a[i]) -> RLE(a[i]+a[j]) m <= n
[  754.409 ms] 863132560 O(m.log(m)) RLE(a[i])+NTT

As you can see I was not too far away from the estimated ~24 sec :).

Here some times to compare with additional fast convolution methods I tried with use of Karatsuba and FastSQR from Fast bignum square computation to avoid FFT/NTT use:

n=10000
[ 749.033 ms] 149252794 O(n^2)        naive
[1077.618 ms] 149252794 O(n'^2)       RLE(a[i])+fast_sqr32
[ 568.510 ms] 149252794 O(n'^1.585)   RLE(a[i])+Karatsuba32
[  65.805 ms] 149252794 O(n'^2)       RLE(a[i]) -> RLE(a[i]+a[j])
[  53.833 ms] 149252794 O(n'.log(n')) RLE(a[i])+FFT
[  34.129 ms] 149252794 O(n'.log(n')) RLE(a[i])+NTT
n=20000
[3084.546 ms] 365847531 O(n^2)        naive
[4311.491 ms] 365847531 O(n'^2)       RLE(a[i])+fast_sqr32
[1672.769 ms] 365847531 O(n'^1.585)   RLE(a[i])+Karatsuba32
[ 238.725 ms] 365847531 O(n'^2)       RLE(a[i]) -> RLE(a[i]+a[j])
[ 115.047 ms] 365847531 O(n'.log(n')) RLE(a[i])+FFT
[  71.587 ms] 365847531 O(n'.log(n')) RLE(a[i])+NTT
n=40000
[12592.250 ms] 347013745 O(n^2)        naive
[17135.248 ms] 347013745 O(n'^2)       RLE(a[i])+fast_sqr32
[5172.836 ms] 347013745 O(n'^1.585)   RLE(a[i])+Karatsuba32
[ 951.256 ms] 347013745 O(n'^2)       RLE(a[i]) -> RLE(a[i]+a[j])
[ 242.918 ms] 347013745 O(n'.log(n')) RLE(a[i])+FFT
[ 152.553 ms] 347013745 O(n'.log(n')) RLE(a[i])+NTT

Sadly the overhead of Karatsuba is too big so threshold is above n=200000 making it useless for this task.

Answer 2

Since ai <= 200.000 and N<=200.000, there might be 40.000.000.000 terms in total, but you know that ai + aj <= 400.000. There can be at most 400.000 unique terms. That's already 5 orders of magnitude better.

However, most of these terms aren't primes; there only ~40.000 primes under 400.000. You may end up with a somewhat higher multiplicity of each individual term, but that's not a big deal. Calculating (prime^N) modulo 1000000007 is fast enough even for big X.

You can reasonably pre-calculate the factorization of all numbers <=400.000 and get the primes <=400.000 as a free side-effect.

This method achieves a speed-up because we delay multiplication, and instead count small prime factors found through a lookup. By the time we need to do the multiplications, we have a series of exponents and can use repeated squaring to efficiently reduce them.

It's counter-intuitive perhaps that we use prime factorization as a speed-up, when the "well-known fact" is that prime factorization is hard. But this is possible because each term is small, and we repeatedly need the same factorization.

[edit] From the comments, it seems that figuring out the multiplicity of ai+aj is hard, since you can only count the terms where i<j. But that's a non-issue. Count the multiplicity of all terms ai+aj, and divide by two since aj+i==ai+aj. This is only wrong for the diagonal where i==j. This is fixed by adding the multiplicity of all terms ai+ai prior to dividing by 2.

Ex: a={1 2 3}, terms to consider are {1+1, 1+2, 1+3, 2+2, 2+3, 3+3} [triangle]. The multiplicity of 4 is 2 (via 1+3 and 2+2). Instead, consider {1+1, 1+2, 1+3, 2+1, 2+2, 2+3, 3+1, 3+2, 3+3} [square] + {1+1, 2+2, 3+3} [diagonal]. The multiplicity of 4 is now 4 (1+3,2+2,3+1 and 2+2), divide by 2 to get the correct result.

And since the order of a[] no longer matters for the square variant, you can use a counting sort on it. E.g. given {4,5,6,5}, we get 4:1, 5:2, 6:1. Thus the multiplicity of 10 is 4+6:1, 5+5:2, 6+4:1