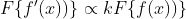We know that the Fourier Transform of a derivative is
where k is the fourier variable. Explanation here
My question is, why doesn't sympy use this knowledge? For example:
from sympy import Function, symbols, fourier_transform, Derivative
f = Function('f')
x, k= symbols('x, k')
G = fourier_transform(Derivative(f(x), x, x) + f(x), x, k)
print(G)
This prints
FourierTransform(f(x), x, k) + FourierTransform(Derivative(f(x), x, x), x, k)
But I expected it to print (up to some factors of 2 pi i)
FourierTransform(f(x), x, k) + k**2 FourierTransform(f(x), x, k)
Is there a way to tell sympy it's save to make this simplification because I expect f(x) -> 0 as x goes to infinity?
If not, what would be the cleanest way to make the substitution?