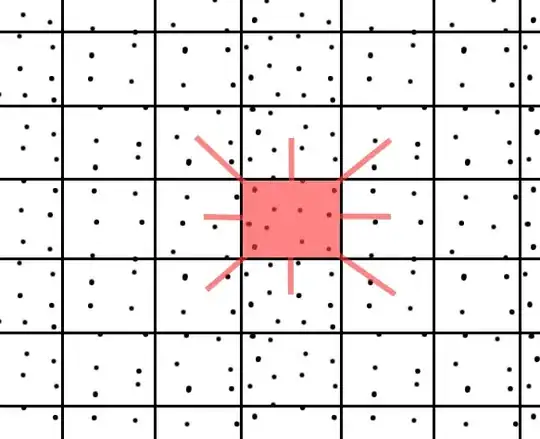
I need to find for each point of the data set all its nearest neighbors. The data set contains approx. 10 million 2D points. The data are close to the grid, but do not form a precise grid...
This option excludes (in my opinion) the use of KD Trees, where the basic assumption is no points have same x coordinate and y coordinate.
I need a fast algorithm O(n) or better (but not too difficult for implementation :-)) ) to solve this problem ... Due to the fact that boost is not standardized, I do not want to use it ...
Thanks for your answers or code samples...