Finding the shortest path nodes with breadth first search

Question

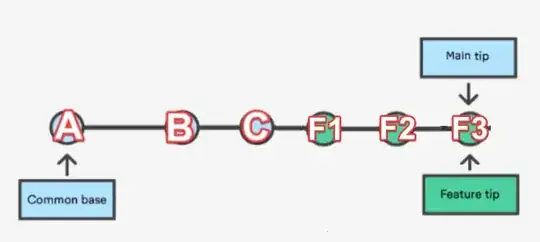
I am running breadth first search on the above graph to find the shortest path from Node 0 to Node 6.

My code

public List<Integer> shortestPathBFS(int startNode, int nodeToBeFound){
        boolean shortestPathFound = false;
        Queue<Integer> queue = new LinkedList<Integer>();
        Set<Integer> visitedNodes = new HashSet<Integer>();
        List<Integer> shortestPath = new ArrayList<Integer>();
        queue.add(startNode);
        shortestPath.add(startNode);

        while (!queue.isEmpty()) {
            int nextNode = queue.peek();
            shortestPathFound = (nextNode == nodeToBeFound) ? true : false;
            if(shortestPathFound)break;
            visitedNodes.add(nextNode);
            System.out.println(queue);
            Integer unvisitedNode = this.getUnvisitedNode(nextNode, visitedNodes);

            if (unvisitedNode != null) {
                    queue.add(unvisitedNode);
                    visitedNodes.add(unvisitedNode);
                    shortestPath.add(nextNode); //Adding the previous node of the visited node 
                    shortestPathFound = (unvisitedNode == nodeToBeFound) ? true : false;
                    if(shortestPathFound)break;
                } else {
                    queue.poll();
                }
        }
        return shortestPath;
    }

I need to track down the nodes through which the BFS algo. traversed to reach node 6, like [0,3,2,5,6]. For that I have created a List named shortestPath & trying to store the previous nodes of the visited nodes, to get the list of nodes. Referred

But it doesn't seem to work. The shortest path is [0,3,2,5,6]

In the list what I get is Shortest path: [0, 0, 0, 0, 1, 3, 3, 2, 5]

It's partially correct but gives the extra 1 .

If I again start from the first element 0 of the shortestPath list & start traversing & backtracking. Like 1 doesn't has an edge to 3, so I backtrack & move from 0 to 3 to 5, I will get the answer but not sure if that's the correct way.

What is the ideal way to getting the nodes for the shortest path?

Answer 1

Storing all the visited nodes in a single list is not helpful for finding the shortest path because in the end you have no way of knowing which nodes were the ones that led to the target node, and which ones were dead ends.

What you need to do is for every node to store the previous node in the path from the starting node.

So, create a map Map<Integer, Integer> parentNodes, and instead of this:

shortestPath.add(nextNode);

do this:

parentNodes.put(unvisitedNode, nextNode);

After you reach the target node, you can traverse that map to find the path back to the starting node:

if(shortestPathFound) {
    List<Integer> shortestPath = new ArrayList<>();
    Integer node = nodeToBeFound;
    while(node != null) {
        shortestPath.add(node)
        node = parentNodes.get(node);
    }
    Collections.reverse(shortestPath);
}

Answer 2

As you can see in acheron55 answer:

"It has the extremely useful property that if all of the edges in a graph are unweighted (or the same weight) then the first time a node is visited is the shortest path to that node from the source node"

So all you have to do, is to keep track of the path through which the target has been reached. A simple way to do it, is to push into the Queue the whole path used to reach a node, rather than the node itself.
The benefit of doing so is that when the target has been reached the queue holds the path used to reach it.
Here is a simple implementation :

/**
 * unlike common bfs implementation queue does not hold a nodes, but rather collections
 * of nodes. each collection represents the path through which a certain node has
 * been reached, the node being the last element in that collection
 */
private Queue<List<Node>> queue;

//a collection of visited nodes
private Set<Node> visited;

public boolean bfs(Node node) {

    if(node == null){ return false; }

    queue = new LinkedList<>(); //initialize queue
    visited = new HashSet<>();  //initialize visited log

    //a collection to hold the path through which a node has been reached
    //the node it self is the last element in that collection
    List<Node> pathToNode = new ArrayList<>();
    pathToNode.add(node);

    queue.add(pathToNode);

    while (! queue.isEmpty()) {

        pathToNode = queue.poll();
        //get node (last element) from queue
        node = pathToNode.get(pathToNode.size()-1);

        if(isSolved(node)) {
            //print path 
            System.out.println(pathToNode);
            return true;
        }

        //loop over neighbors
        for(Node nextNode : getNeighbors(node)){

            if(! isVisited(nextNode)) {
                //create a new collection representing the path to nextNode
                List<Node> pathToNextNode = new ArrayList<>(pathToNode);
                pathToNextNode.add(nextNode);
                queue.add(pathToNextNode); //add collection to the queue
            }
        }
    }

    return false;
}

private List<Node> getNeighbors(Node node) {/* TODO implement*/ return null;}

private boolean isSolved(Node node) {/* TODO implement*/ return false;}

private boolean isVisited(Node node) {
    if(visited.contains(node)) { return true;}
    visited.add(node);
    return false;
}

This is also applicable to cyclic graphs, where a node can have more than one parent.

Answer 3

In addition to the already given answer by user3290797.

It looks like You are dealing with an unweighted graph. We interpret this as every edge has a weight of 1. In this case, once You have associated a distance to the root node with every node of the graph (the breadth-first traversal), it becomes trivial to reconstruct the shortest path from any node, and even detect if there are multiple ones.

All You need to do is a breadth- (in case You want every shortest path) or depth-first traversal of the same graph starting from the target node and only considering neighbours with a depth's value of exactly 1 less.

So we need to jump from distance 4 (node 6) to 3, 2, 1, 0, and there is only one way (in this case) to do so.

In case we are interested in the shortest path to node 4 the result would be distances 2-1-0 or nodes 4-3-0 or 4-8-0.

BTW, this approach can easily be modified to work with weighted graphs (with non-negative weights) too: valid neighbours are those with distance equals to current minus the weight of the edge -- this involves some actual calculations and directly storing previous nodes along the shortest path might be better.