How good is this interpolation method?

Question

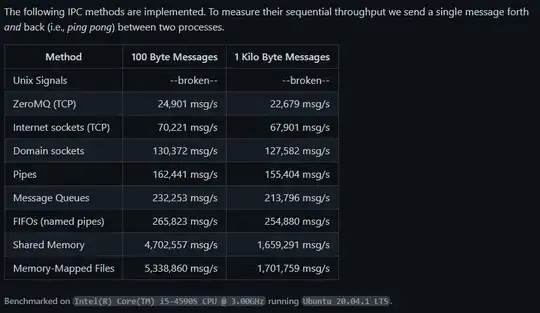
I came up with a custom interpolation method for my problem and I'd like to ask if there are any risks using it. I am not a math or programming expert, that's why I'd like a feedback :)

Story:

I was searching for a good curve-fit method for my data when I came up with an idea to interpolate the data.

I am mixing paints together and making reflectance measurements with a spectrophotometer when the film is dry. I would like to calculate the required proportions of white and colored paints to reach a certain lightness, regardless of any hue shift (e.g. black+white paints gives a bluish grey) or chroma loss (e.g. orange+white gives "pastel" yellowish orange, etc.)

I check if Beer-Lambert law applies, but it does not. Pigment-mixing behaves in a more complicated fashion than dye-dilutions. So I wanted to fit a curve to my data points (the process is explained here: Interpolation for color-mixing

First step was doing a calibration curve, I tested the following ratios of colored VS white paints mixed together:

ratios = 1, 1/2., 1/4., 1/8., 1/16., 1/32., 1/64., 0

This is the plot of my carefully prepared samples, measured with a spectrophotometer, the blue curve represents the full color (ratio = 1), the red curve represents the white paint (ratio = 0), the black curves the mixed samples:

Second step I wanted to guess from this data a function that would compute a spectral curve for any ration between 0 and 1. I did test several curve fitting (fitting an exponential function) and interpolation (quadratic, cubic) methods but the results were of a poor quality.

For example, this is my reflectance data at 380nm for all the color samples:

This is the result of scipy.optimize.curve_fit using the function:

def func(x, a, b, c):
    return a * np.exp(-b * x) + c

popt, pcov = curve_fit(func, x, y)

Then I came-up with this idea: the logarithm of the spectral data gives a closer match to a straight line, and the logarithm of the logarithm of the data is almost a straight line, as demonstrated by this code and graph:

import numpy as np
import matplotlib.pyplot as plt 

reflectance_at_380nm = 5.319, 13.3875, 24.866, 35.958, 47.1105, 56.2255, 65.232, 83.9295
ratios = 1, 1/2., 1/4., 1/8., 1/16., 1/32., 1/64., 0

linear_approx = np.log(np.log(reflectance_at_380nm))

plt.plot(ratios, linear_approx)
plt.show()

What I did then is to interpolate the linear approximation an then convert the data back to linear, then I got a very nice interpolation of my data, much better than what I got before:

import numpy as np
import matplotlib.pyplot as plt 
import scipy.interpolate 

reflectance_at_380nm = 5.319, 13.3875, 24.866, 35.958, 47.1105, 56.2255, 65.232, 83.9295
ratios = 1, 1/2., 1/4., 1/8., 1/16., 1/32., 1/64., 0

linear_approx = np.log(np.log(reflectance_at_380nm))

xnew = np.arange(100)/100.

cs = scipy.interpolate.spline(ratios, linear_approx, xnew, order=1)
cs = np.exp(np.exp(cs))

plt.plot(xnew,cs)
plt.plot(x,y,'ro')
plt.show()

So my question is for experts: how good is this interpolation method and what are the risks of using it? Can it lead to wrong results?

Also: can this method be improved or does it already exists and if so how is it called?

Thank you for reading

Answer 1

This looks similar to the Kernel Method that is used for fitting regression lines or finding decision boundaries for classification problems.

The idea behind the Kernel trick being, the data is transformed into a dimensional space (often higher dimensional), where the data is linearly separable (for classification), or has a linear curve-fit (for regression). After the curve-fitting is done, inverse transformations can be applied. In your case successive exponentiations (exp(exp(X))), seems to be the inverse transformation and successive logarithms (log(log(x)))seems to be the transformation.

I am not sure if there is a kernel that does exactly this, but the intuition is similar. Here is a medium article explaining this for classification using SVM: https://medium.com/@zxr.nju/what-is-the-kernel-trick-why-is-it-important-98a98db0961d

Since it is a method that is quite popularly used in Machine Learning, I doubt it will lead to wrong results if the fit is done properly (not under-fit or over-fit) - and this needs to be judged by statistical testing.