75

What are the pros and cons of using System.Security.Cryptography.RNGCryptoServiceProvider vs System.Random. I know that RNGCryptoServiceProvider is 'more random', i.e. less predictable for hackers. Any other pros or cons?

UPDATE:

According to the responses, here are the pros and cons of using RNGCryptoServiceProvider so far:

Pros

  • RNGCryptoServiceProvider is a stronger cryptographically random number, meaning it would be better for determining encryption keys and the likes.

Cons

  • Random is faster because it is a simpler calculation; when used in simulations or long calculations where cryptographic randomness isn't important, this should be used. Note: see Kevin's answer for details about simulations - Random is not necessarily random enough, and you may want to use a different non-cryptographic PRNG.
configurator
  • 40,828
  • 14
  • 81
  • 115

4 Answers4

56

A cryptographically strong RNG will be slower --- it takes more computation --- and will be spectrally white, but won't be as well suited to simulations or Monte Carlo methods, both because they do take more time, and because they may not be repeatable, which is nice for testing.

In general, you want to use a cryptographic PRNG when you want a unique number like a UUID, or as a key for encryption, and a deterministic PRNG for speed and in simulation.

Charlie Martin
  • 110,348
  • 25
  • 193
  • 263
  • 1
    e.g. Blum Blum Shub vs Mersenne Twister. BBS is created with a strong cryptographical proof in mind, and to get anywhere near random for a non-crypto purpose, it's way too slow and resource intensive. – Calyth Jan 07 '09 at 01:17
  • Re testing, you can always use Random while testing and change the implementation to use RNGCryptoServiceProvider in production, can't you? – configurator Jan 08 '09 at 01:26
  • You can, but a strong PRNG still won't be as suitable for some purposes like Monte Carlo; repeatability and speed are desirable in production use too. – Charlie Martin Jan 08 '09 at 03:55
  • What do you mean by "spectrally white"? – Robert MacLean May 28 '13 at 10:04
  • Like white noise. The power spectrum is flat, and there are no groups of numbers that are more probable than others. See http://en.wikipedia.org/wiki/White_noise and http://en.wikipedia.org/wiki/Power_spectral_density Basically, it's a strong test for really random numbers. – Charlie Martin May 29 '13 at 13:36
  • 2
    @CharlieMartin "The power spectrum is flat, and there are no groups of numbers that are more probable". Wouldn't the fact that the spectrum is flat mean that some groups of numbers *are* more likely to show up? In RNGCryptoServiceProvider, each bit has roughly a 50% chance to be set, this means that numbers with roughly half their bits set will be the most popular, and numbers with only a few bits set (or values with all their bits set) will be highly improbable. – josh poley Sep 08 '15 at 20:42
  • Ooh, nice question. Consider: `001100` has the same number of bits set as `110000`. And see this: https://en.wikipedia.org/wiki/Statistical_randomness – Charlie Martin Sep 08 '15 at 20:53
  • @joshpoley: I know this is old, but: The set of numbers with half the bits set to 1 has far more values than the set of numbers with only one bit set to 1. If each number is equally probable, then you're far more likely to see a number from the first set than the second set since the first set is so much larger. That we're more likely to get a number from the first set is exactly balanced by each number in the set being less likely to be selected given we've selected from that set. – MichaelS Jan 25 '22 at 22:31
  • @MichaelS, Unless implementations have changed, they don't guarantee that each "number" has equal probability, they guarantee that each "bit" has equal probability. The generators spit out a stream of bytes, and at the time of generation they don't know how many will be needed for the size your number. Specific implementations could certainly place a post filter on that stream to finesse output, for example if you want a "normal" distribution (for non-cryptographic uses). – josh poley Jan 26 '22 at 16:39
12

System.Random is not thread safe.

John Smith
  • 7,243
  • 6
  • 49
  • 61
Yury Chaikou
  • 143
  • 1
  • 5
  • Good point. You can see http://blogs.msdn.com/pfxteam/archive/2009/02/19/9434171.aspx for further discussion. – configurator Feb 03 '10 at 01:51
  • 4
    Now that I think about it, RNGCryptoServiceProvider isn't either! – configurator Feb 03 '10 at 01:52
  • 10
    MSDN seems to say that RNGCryptoServiceProvider is thread safe (http://msdn.microsoft.com/en-us/library/system.security.cryptography.rngcryptoserviceprovider.aspx). – Scott Lawrence Jun 17 '10 at 19:55
  • 4
    Joking aside, it can corrupt itself and return zeroes (http://stackoverflow.com/a/11109361/155892). (http://dilbert.com/strips/comic/2001-10-25/) – Mark Sowul May 08 '13 at 15:09
10

Yes, there is only one more. As Charlie Martin wrote System.Random is faster.

I would like to add the following info:

The RNGCryptoServiceProvider is the default implementation of a security standards compliant random number generator. If you need a random variable for security purposes, you must use this class, or an equivalent, but don't use System.Random because it is highly predictable.

For all other uses the higher performance of System.Random, and equivalent classes, are welcome.

John Smith
  • 7,243
  • 6
  • 49
  • 61
Jader Dias
  • 88,211
  • 155
  • 421
  • 625
  • can i use rngcryptoserviceprovider as an authentication token for a webapi consumed by different applications. – Dragon Mar 30 '17 at 16:44
8

In addition to the prior answers:

System.Random should NEVER be used in simulations or numerical solvers for science and engineering, where there are material negative consequences of inaccurate simulation results or convergence failure. This is because Microsoftʼs implementation is deeply flawed in several respects, and they cannot (or will not) easily fix it due to compatibility issues. See this post.

So:

  • If there is an adversary who shouldnʼt know the generated sequence, then use RNGCryptoServiceProvider or another carefully designed, implemented and validated cryptographically strong RNG, and ideally use hardware randomness where possible. Otherwise;

  • If it is an application such as a simulation that requires good statistical properties, then use a carefully designed and implemented non‑crypto PRNG such as the Mersenne Twister. (A crypto RNG would also be correct in these cases, but often too slow and unwieldy.) Otherwise;

  • ONLY if the use of the numbers is completely trivial, such as deciding which picture to show next in a randomized slideshow, then use System.Random.

I recently encountered this issue very tangibly when working on a Monte Carlo simulation intended to test the effects of different usage patterns for medical devices. The simulation produced results that went mildly in the opposite direction of what would have been reasonably expected.

Sometimes when you canʼt explain something, thereʼs a reason behind it, and that reason could be very onerous!

Hereʼs a plot of the p‑values that were obtained over an increasing number of simulation batches:

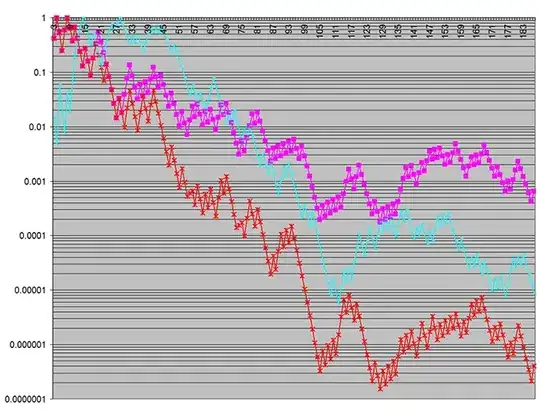
Input & output _p_‑values while using <code>System.Random</code>

The red and magenta plots show the statistical significance of differences between the two usage models in two output metrics under study.

The cyan plot is a particularly shocking result, because it represents p‑values for a characteristic of the random input to the simulation. (This was being plotted just to confirm the input wasnʼt faulty.) The input was, of course, by design the same between the two usage models under study, so there should not have been any statistically significant difference between the input to the two models. Yet here I was seeing better than 99.97% confidence that there was such a difference!!

Initially I thought there was something wrong in my code, but everything checked out. (In particular I confirmed that threads were not sharing System.Random instances.) When repeated testing found this unexpected result to be highly consistent, I started suspecting System.Random.

I replaced System.Random with a Mersenne Twister implementation — no other changes, — and immediately the output became drastically different, as shown here:

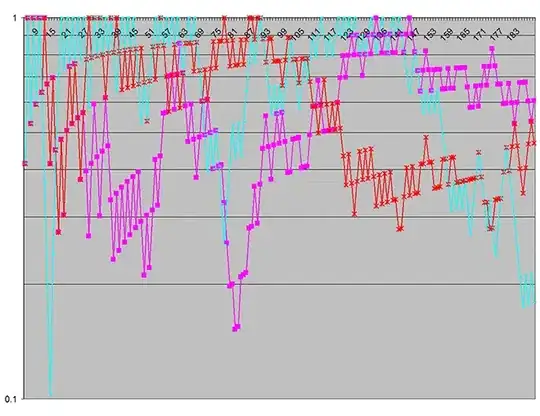
Input & output _p_‑values after switching to a better PRNG

This chart reflects there being no statistically significant difference between the two usage models for the parameters being used in this particular test set. This was an expected result.

Note that in the first chart, the vertical log scale (on the p‑value) covers seven decades, whereas there is only a single decade in the second — demonstrating just how pronounced the statistical significance of the spurious discrepancies was! (The vertical scale indicates the probability the discrepancies could have arisen by chance.)

I suspect what was happening was that System.Random has some correlations over some fairly short generator cycle, and different patterns of internal randomness sampling between the two models under test (which had substantially different numbers of calls to Random.Next) caused these to affect the two models in distinct ways.

It so happens that the simulation input draws from the same RNG streams as the models use for internal decisions, and this apparently caused these sampling discrepancies to impact the input. (This was actually a lucky thing, because otherwise I may not have realized that the unexpected result was a software fault and not some real property of the devices being simulated!)

Kevin
  • 1,179
  • 7
  • 18