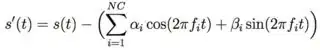I have the time series below
I want to check for cycles in order to remove them (as part of the usual pre-processing of time series), so I apply FFT.
# Number of samplepoints
N = len(y)
# sample spacing
T = 1.0 # 1 day
x = np.linspace(0.0, N*T, N)
yf = scipy.fftpack.fft(y)
xf = np.linspace(0.0, 1.0/(2.0*T), N/2)
components = 2.0/N * np.abs(yf[:N//2])
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.plot(xf, components)
This results in the following plot.
I want to remove the four greatest components. In order to do this I'm implementing the formula below.
max_components = sorted(components, reverse=True)[:4]
idx_max_comp = []
for comp in max_components:
for i in range(len(components)):
if components[i] == comp:
idx_max_comp.append(i)
break
cycle_signal = np.zeros(len(y))
for idx in idxs:
a, b = (2.0/N) * np.real(yf[idx]), (2.0/N) * np.imag(yf[idx])
fi = xf[idx]
cycle_signal += (a * np.cos(2 * np.pi * fi * x)) + (b * np.sin(2 * np.pi * fi * x))
y = y - cycle_signal
But when I apply FFT again it's easy to see it didn't work.
Why?