I'm solving the following problem: I have an object and I know its position now and its position 300ms ago. I assume the object is moving. I have a point to which I want the object to get.
What I need is to get the angle from my current object to the destination point in such a format that I know whether to turn left or right.
The idea is to assume the current angle from the last known position and the current position.
I'm trying to solve this in MATLAB. I've tried using several variations with atan2 but either I get the wrong angle in some situations (like when my object is going in circles) or I get the wrong angle in all situations.
Examples of code that screws up:
a = new - old;
b = dest - new;
alpha = atan2(a(2) - b(2), a(1) - b(1);
where new is the current position (eg. x = 40; y = 60; new = [x y];), old is the 300ms old position and dest is the destination point.
Edit
Here's a picture to demonstrate the problem with a few examples:
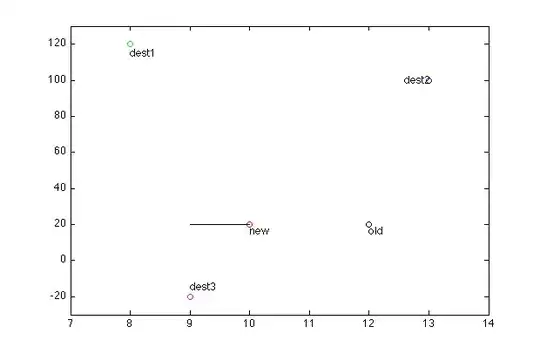
In the above image there are a few points plotted and annotated. The black line indicates our estimated current facing of the object.
If the destination point is dest1 I would expect an angle of about 88°.
If the destination point is dest2 I would expect an angle of about 110°.
If the destination point is dest3 I would expect an angle of about -80°.