Derivatives of a spline: `scipy splev`

Question

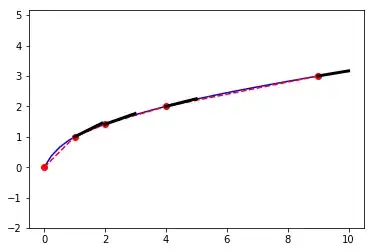
I'm trying to find derivatives of a spline at several points using splev in scipy. For example:

import numpy as np
from scipy.interpolate import splprep, splev
import matplotlib.pyplot as plt

# function to normalize each row
def normalized(a, axis=-1, order=2):
    l2 = np.atleast_1d(np.linalg.norm(a, order, axis))
    l2[l2==0] = 1
    return a / np.expand_dims(l2, axis)

# points and spline
pts = np.array([[0,0],[1,1],[2,np.sqrt(2)],[4,2],[9,3]])
tck, u = splprep(pts.T, u=None, k=3, s=0.0, per=0)

# compute new points and derivatives
u_new = np.linspace(u.min(), u.max(), 5*u.shape[0])
x_new, y_new = splev(u_new, tck, der=0)
xp_num, yp_num = splev(pts, tck, der=1) # numerical derivatices
xp_the, yp_the= pts[1:,0], 0.5/np.sqrt(pts[1:,0]) # analytical derivatives
R = normalized(yp_num/xp_num)
X,Y = pts[1:,0], pts[1:,1]
U,V = X + R[1:,0], Y+R[1:,1]

I'd like to plot the tangents at the given point:

plt.plot(x_new,y_new,'-b')
plt.plot(pts[:,0],pts[:,1],'--ro')
plt.quiver(X,Y,U,V, angles='xy', scale_units='xy')

I think these tangent lines are wrong. My understanding was that xp_num and yp_num are numerical derivatives of the spline with respect to x and y. So to find dy/dx, I should simply divide them. Is this correct?

Eventually, I'd like to find tangents of a curve like this

@PaulPanzer: It normalizes each row. I added the definition of `normalize`. — Mahdi, Feb 18 '17 at 07:42
Strange, your code looks to me as if it shouldn't create any vectors in the plot at all. `yp_num` and `xp_num` are 1d, aren't they? So your `R` should be 1 x something, so when you are slicing `R[1:,0] you should get an empty array. Am I missing something here? — Paul Panzer, Feb 18 '17 at 08:06
@PaulPanzer: The shape of `yp_num` and `xp_num` is `(5,2)` which confuses me! — Mahdi, Feb 19 '17 at 03:39
Of, course, that's the bug! You are passing pts as the first parameter to splev, which is complete and utter nonsense! — Paul Panzer, Feb 19 '17 at 03:59

Paul Panzer · Answer 1 · 2017-02-18T02:53:39.433

Your problem (the obviously wrong derivatives) is not related to the numerical derivative since you are not using them at least in the code you posted. What is clearly wrong unless your normalized function does something truly magic is your dividing yp_the by xp_the since the former is indeed the increment, the latter is not it should be constant to get

dy
--
dx

as opposed to your

 dy
----
x dx

You were probably coming from the formula for a parametric curve

.     dy
      --
dy    dt
-- = ----
dx    dx
      --
      dt

used t=x and then overlooked that dx/dx is constant. Kind of thing that happens to the best of us.

Awesome, that's exactly right I thought about parametric curve! Thanks! — Mahdi, Feb 18 '17 at 07:47

score 1 · Answer 2 · answered Feb 18 '17 at 02:27

you didn't include your R = normalized(yp_the/xp_the) source

I did it with linalg.norm

then I changed the delta_Y for the normalized derivative

and gave up on quiver

import numpy as np
from scipy.interpolate import splprep, splev
import matplotlib.pyplot as plt

# points and spline
pts = np.array([[0,0],[1,1],[2,np.sqrt(2)],[4,2],[9,3]])
tck, u = splprep(pts.T, u=None, k=3, s=0.0, per=0)

# compute new points and derivatives
u_new = np.linspace(u.min(), u.max(), 5*u.shape[0])
x_new, y_new = splev(u_new, tck, der=0)
xp_num, yp_num = splev(pts, tck, der=1) # numerical derivatices
xp_the, yp_the= pts[1:,0], 0.5/np.sqrt(pts[1:,0]) # analytical derivatives
#R = normalized(yp_the/xp_the)
N = np.linalg.norm(np.array([xp_the, yp_the]), axis=0)

X,Y = pts[1:,0], pts[1:,1]
#U,V = X + R[1:,0], Y+R[1:,1]
U,V = X + xp_the/N, Y + X*yp_the/N # delta Y = dy/dx * x

plt.axes().set_aspect('equal', 'datalim')

plt.plot(x_new,y_new,'-b')
plt.plot(pts[:,0],pts[:,1],'--ro')
#plt.quiver(X,Y,U,V, scale=10, pivot='mid')# angles='xy', scale_units=’xy’, scale=1

plt.plot((X, U), (Y, V), '-k', lw=3)

Sorry about my mistake. I meant to plot the tangents using `xp_num` and `yp_num`. — Mahdi, Feb 18 '17 at 07:50

Derivatives of a spline: `scipy splev`

2 Answers2