I realize this is question is almost 4 years old and already has an answer, but I wanted to chime in with some additional information for the sake of anyone who comes across this question in the future. Specifically, I want to try to answer 2 questions:
- how are multiple Selects that return single values combined to create a single Select that returns a sequence of values?
- is it possible to return early when a solution path is destined to fail?
Chaining Selects
Select is implemented as a monad transformer in the transformers library (go figure), but let's take a look at how one might implement >>= for Select by itself:
(>>=) :: Select r a -> (a -> Select r b) -> Select r b
Select g >>= f = Select $ \k ->
let choose x = runSelect (f x) k
in choose $ g (k . choose)
We start by defining a new Select which takes an input k of type a -> r (recall that Select wraps a function of type (a -> r) -> a). You can think of k as a function that returns a "score" of type r for a given a, which the Select function may use to determine which a to return.
Inside our new Select, we define a function called choose. This function passes some x to the function f, which is the a -> m b portion of monadic binding: it transforms the result of the m a computation into a new computation m b. So f is going to take that x and return a new Select, which choose then runs using our scoring function k. You can think of choose as a function that asks "what would the final result be if I selected x and passed it downstream?"
On the second line, we return choose $ g (k . choose). The function k . choose is the composition of choose and our original scoring function k: it takes in a value, calculates the downstream result of selecting that value, and returns the score of that downstream result. In other words, we've created a kind of "clairvoyant" scoring function: instead of returning the score of a given value, it returns the score of the final result we would get if we selected that value. By passing in our "clairvoyant" scoring function to g (the original Select that we're binding to), we're able to select the intermediate value that leads to the final result we're looking for. Once we have that intermediate value, we simply pass it back into choose and return the result.
That's how we're able to string together single-value Selects while passing in a scoring function that operates on an array of values: each Select is scoring the hypothetical final result of selecting a value, not necessarily the value itself. The applicative instance follows the same strategy, the only difference being how the downstream Select is computed (instead of passing a candidate value into the a -> m b function, it maps a candidate function over the 2nd Select.)
Returning Early
So, how can we use Select while returning early? We need some way of accessing the scoring function within the scope of the code that constructs the Select. One way to do that is to construct each Select within another Select, like so:
sequenceSelect :: Eq a => [a] -> Select Bool [a]
sequenceSelect [] = return []
sequenceSelect domain@(x:xs) = select $ \k ->
if k [] then runSelect s k else []
where
s = do
choice <- elementSelect (x:|xs)
fmap (choice:) $ sequenceSelect (filter (/= choice) domain)
This allows us to test the sequence in progress and short-circuit the recursion if it fails. (We can test the sequence by calling k [] because the scoring function includes all of the prepends that we've recursively lined up.)
Here's the whole solution:
import Data.List
import Data.List.NonEmpty (NonEmpty(..))
import Control.Monad.Trans.Select
validBoard :: [Int] -> Bool
validBoard qs = all verify (tails qs)
where
verify [] = True
verify (x:xs) = and $ zipWith (\i y -> x /= y && abs (x - y) /= i) [1..] xs
nqueens :: Int -> [Int]
nqueens boardSize = runSelect (sequenceSelect [1..boardSize]) validBoard
sequenceSelect :: Eq a => [a] -> Select Bool [a]
sequenceSelect [] = return []
sequenceSelect domain@(x:xs) = select $ \k ->
if k [] then runSelect s k else []
where
s = do
choice <- elementSelect (x:|xs)
fmap (choice:) $ sequenceSelect (filter (/= choice) domain)
elementSelect :: NonEmpty a -> Select Bool a
elementSelect domain = select $ \p -> epsilon p domain
-- like find, but will always return something
epsilon :: (a -> Bool) -> NonEmpty a -> a
epsilon _ (x:|[]) = x
epsilon p (x:|y:ys) = if p x then x else epsilon p (y:|ys)
In short: we construct a Select recursively, removing elements from the domain as we use them and terminating the recursion if the domain has been exhausted or if we're on the wrong track.
One other addition is the epsilon function (based on Hilbert's epsilon operator). For a domain of size N it will check at most N - 1 items... it might not sound like a huge savings, but as you know from the above explanation, p will usually kick off the remainder of the entire computation, so it's best to keep predicate calls to a minimum.
The nice thing about sequenceSelect is how generic it is: it can be used to create any Select Bool [a] where
- we're searching within a finite domain of distinct elements
- we want to create a sequence that includes every element exactly once (i.e. a permutation of the domain)
- we want to test partial sequences and abandon them if they fail the predicate
Hope this helps clarify things!
P.S. Here's a link to an Observable notebook in which I implemented the Select monad in Javascript along with a demonstration of the n-queens solver: https://observablehq.com/@mattdiamond/the-select-monad
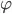and turn the SAT solver into a N-queens solver.