Plotting both a GLM and LM of same data

Question

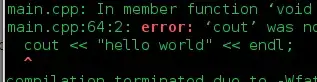
I would like to plot both a linear model (LM) and non-linear (GLM) model of the same data.

The range between 16% - 84% should line up between a LM and GLM, Citation: section 3.5

I have included a more complete chunk of the code because I am not sure at which point I should try to cut the linear model. or at which point I have messed up - I think with the linear model.

The code below results in the following image:

My Objective (taken from previous citation-link).

Here is my data:

mydata3 <- structure(list(
               dose = c(0, 0, 0, 3, 3, 3, 7.5, 7.5, 7.5, 10,     10, 10, 25, 25, 25, 50, 50, 50), 
               total = c(25L, 25L, 25L, 25L, 25L, 25L, 25L, 25L, 25L, 25L, 25L, 25L, 25L, 25L, 25L, 25L, 25L, 25L), 
               affected = c(1, 0, 1.2, 2.8, 4.8, 9, 2.8, 12.8, 8.6, 4.8, 4.4, 10.2, 6, 20, 14, 12.8, 23.4, 21.6), 
               probability = c(0.04, 0, 0.048, 0.112, 0.192, 0.36, 0.112, 0.512, 0.344, 0.192, 0.176, 0.408, 0.24, 0.8, 0.56, 0.512, 0.936, 0.864)), 
               .Names = c("dose", "total", "affected", "probability"), 
               row.names = c(NA, -18L), 
               class = "data.frame")

My script:

#load libraries

library(ggplot2)
library(drc)  # glm model
library(plyr) # rename function
library(scales) #log plot scale

#Creating linear model
mod_linear <- lm(probability ~ (dose), weights = total, data = mydata3)

#Creating data.frame: note values 3 and 120 refer to 16% and 84% response in sigmoidal plot
line_df <-expand.grid(dose=exp(seq(log(3),log(120),length=200)))

#Extracting values from linear model
p_line_df <- as.data.frame(cbind(dose = line_df,
                               predict(mod_linear, newdata=data.frame(dose = line_df),
                                       interval="confidence",level=0.95)))

#Renaming linear df columns
p_line_df <-rename(p_line_df, c("fit"="probability"))
p_line_df <-rename(p_line_df, c("lwr"="Lower"))
p_line_df <-rename(p_line_df, c("upr"="Upper"))
p_line_df$model <-"Linear"


#Create sigmoidal dose-response curve using drc package
    mod3 <- drm(probability ~ (dose), weights = total, data = mydata3, type ="binomial", fct=LL.2(names=c("Slope:b","ED50:e")))

    #data frame for ggplot2 
    base_DF_3 <-expand.grid(dose=exp(seq(log(1.0000001),log(10000),length=200)))

    #extract data from model
    p_df3 <- as.data.frame(cbind(dose = base_DF_3,
                                 predict(mod3, newdata=data.frame(dose = base_DF_3),
                                         interval="confidence", level=.95)))

#renaming columns
p_df3 <-rename(p_df3, c("Prediction"="probability"))
p_df3$model <-"Sigmoidal" 

#combining Both DataFames
 p_df_all <- rbind(p_df3, p_line_df)

#plotting
ggplot(p_df_all, aes(x=dose,y=probability, group=model))+
    geom_line(aes(x=dose,y=probability,group=model,linetype=model),show.legend = TRUE)+
  scale_x_log10(breaks = c(0.000001, 10^(0:10)),labels = c(0, math_format()(0:10)))

@SandipanDey: Because it is linear on a transformed scale. Hence the term "generalized"? — IRTFM, Feb 24 '17 at 19:28
@42- I thought whether a model is linear or non-linear is decided on the nature of the decision boundary (if a classification model), e.g., logistic regression is a linear model, since the decision boundary is linear, that we can prove mathematically. — Sandipan Dey, Feb 24 '17 at 19:30
It looks like you fit a linear model of `probability` vs `dose`. However, you are plotting dose on the `log10` scale. Wanting the line on the graph to be straight when the x axis is on the `log10` scale implies your linear model should be `probability` vs `log10(dose)`. — aosmith, Feb 24 '17 at 19:50
@SandipanDey: the model is linear in that is uses a linear link function (y=mx+b). Sigmoidal logit /probit models are not linear in traditional sense as they plot non-linear relationships. e.g. mortality at a high dosage is not necessarily going to have the same relation as mortality with a medium dosage. GLMs are a tricky middle ground between non-linear and linear models. — Arch, Feb 25 '17 at 20:28
@aosmith that addresses potential error. but even plotting on a non-log x axis the problem persists. modeling the data with a log10(dose) actually makes some strange shapes. an aside, the logit is not modeled with a log-dose. It is easy to do such, but the non-log dosage were used to make the logit model in order to keep things simple. No real benefit exists in this case for transformation — Arch, Feb 25 '17 at 20:35

dww · Accepted Answer · 2017-02-27T04:47:01.673

Looking at the reference you provided, what the authors describe is the use of a linear model to approximate the central portion of a (sigmoidal) logistic function. The linear model that achieves this is a straight line that passes through the inflection point of the logistic curve, and has the same slope as the logistic function at that inflection point. We can use some basic algebra and calculus to solve this problem.

From ?LL.2, we see that the form of the logistic function being fitted by drm is

f(x) = 1 / {1 + exp(b(log(x) - log(e)))}

We can get the values of the coefficient in this equation by

b = mod3$coefficients[1]
e = mod3$coefficients[2]

Now, by differentiation, the slope of the logistic function is given by

dy/dx = -(b * exp((log(x)-log(e))*b)) / (1+exp((log(x)-log(e))*b))^2

At the inflection point, the dose (x) is equal to the coefficient e, thus the slope at the inflection point simplifies (greatly) to

sl50 = -b/4

Since we also know that the inflection point occurs at the point where probability = 0.5 and dose = e, we can construct the straight line (in log-transformed coordinates) like this:

linear_probability = sl50 * (log(p_df3$dose) - log(e)) + 0.5

Now, to plot the logistic and linear functions together:

p_df3_lin = p_df3
p_df3_lin$model = 'linear'
p_df3_lin$probability = linear_probability

p_df_all <- rbind(p_df3, p_df3_lin)

ggplot(p_df_all, aes(x=dose,y=probability, group=model))+
  geom_line(aes(x=dose,y=probability,group=model,linetype=model),show.legend = TRUE)+
  scale_x_log10(breaks = c(0.000001, 10^(0:10)),labels = c(0, math_format()(0:10))) +
  scale_y_continuous(limits = c(0,1))

This is a great deconstruction of my problem - works perfectly! Thank you! . just a quick followup question: Do you have any idea how/why my linear code resulted in a curved plot? `mod_linear <- lm(probability ~ (dose), weights = total, data = mydata3)` `p_line_df <- as.data.frame(cbind(dose = line_df, predict(mod_linear, newdata=data.frame(dose = line_df), interval="confidence",level=0.95)))` — Arch, Mar 02 '17 at 14:35
@Arch, - you fitted the line in untransformed coordinates, then plotted it on a log scale. Thats why it looks curved. Try this and you'll see what I mean: `plot(1:100, 1:100, type='l', log = 'x')` — dww, Mar 02 '17 at 14:39

Plotting both a GLM and LM of same data

1 Answers1