Dijkstra with negative edges. Don't understand the examples, they work according to CLRS pseudocode

Question

EDIT 2: It seems this isn't from CLRS (I assumed it was because it followed the same format of CLRS code that was given to us in this Algos and DS course). Still, in this course we were given this code as being "Dijkstra's Algorithm".

I read Why doesn't Dijkstra's algorithm work for negative weight edges? and Negative weights using Dijkstra's Algorithm (second one is specific to the OP's algorithm I think).

Looking at the Pseudocode from CLRS ("Intro to Algorithms"), I don't understand why Dijkstra wouldn't work on those examples of graphs with negative edges.

In the pseudocode (below), we Insert nodes back onto the heap if the new distance to them is shorter than the previous distance to them, so it seems to me that the distances would eventually be updated to the correct distances.

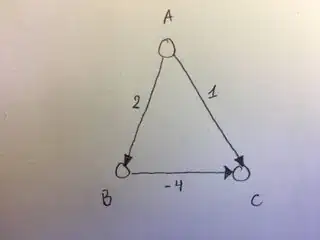
For example:

The claim here is that (A,C) will be set to 1 and never updated to the correct distance -2.

But the pseudocode from CLRS says that we first put C and B on the Heap with distances 1 and 2 respectively; then we pop C, see no outgoing edges; then we pop B, look at the edge (B,C), see that Dist[C] > Dist[B] + w(B,C), update Dist[C] to -2, put C back on the heap, see no outgoing edges and we're done. So it worked fine.

Same for the example in the first answer to this question: Negative weights using Dijkstra's Algorithm

The author of the answer claims that the distance to C will not be updated to -200, but according to this pseudocode that's not true, since we would put B back on the heap and then compute the correct shortest distance to C.

(pseudocode from CLRS)

Dijkstra(G(V, E, ω), s ∈ V )
for v in V do 
    dist[v] ← ∞ 
    prev[v] ← nil
end for
dist[s] = 0 
H←{(s,0)} 
while H̸=∅ do
    v ← DeleteMin(H) 
    for (v, w) ∈ E do
        if dist[w] > dist[v] + ω(v, w) then 
            dist[w] ← dist[v] + ω(v, w) 
            prev[w] ← v
            Insert((w, dist[w]), H)
        end if 
    end for
end while

EDIT: I understand that we assume that once a node is popped off the heap, the shortest distance has been found; but still, it seems (according to CLRS) that we do put nodes back on the heapif the distance is shorter than previously computed, so in the end when the algorithm is done running we should get the correct shortest distance regardless.

Answer 1

That implementation is technically not Dijkstra's algorithm, which is described by Dijkstra here (could not find any better link): the set A he talks about are the nodes for which the minimum path is known. So once you add a node to this set, it's fixed. You know the minimum path to it, and it no longer participates in the rest of the algorithm. It also talks about transferring nodes, so they cannot be in two sets at once.

This is in line with Wikipedia's pseudocode:

 1  function Dijkstra(Graph, source):
 2
 3      create vertex set Q
 4
 5      for each vertex v in Graph:             // Initialization
 6          dist[v] ← INFINITY                  // Unknown distance from source to v
 7          prev[v] ← UNDEFINED                 // Previous node in optimal path from source
 8          add v to Q                          // All nodes initially in Q (unvisited nodes)
 9
10      dist[source] ← 0                        // Distance from source to source
11      
12      while Q is not empty:
13          u ← vertex in Q with min dist[u]    // Node with the least distance will be selected first
14          remove u from Q 
15          
16          for each neighbor v of u:           // where v is still in Q.
17              alt ← dist[u] + length(u, v)
18              if alt < dist[v]:               // A shorter path to v has been found
19                  dist[v] ← alt 
20                  prev[v] ← u 
21
22      return dist[], prev[]

And its heap pseudocode as well.

However, note that Wikipedia also states, at the time of this answer:

Instead of filling the priority queue with all nodes in the initialization phase, it is also possible to initialize it to contain only source; then, inside the if alt < dist[v] block, the node must be inserted if not already in the queue (instead of performing a decrease_priority operation).[3]:198

Doing this would still lead to reinserting a node in some cases with negative valued edges, such as the example graph given in the accepted answer to the second linked question.

So it seems that some authors make this confusion. In this case, they should clearly state that either this implementation works with negative edges or that it's not a proper Dijkstra's implementation.

I guess the original paper might be interpreted as a bit vague. Nowhere in it does Dijkstra make any mention of negative or positive edges, nor does he make it clear beyond any alternative interpretation that a node cannot be updated once in the A set. I don't know if he himself further clarified things in any subsequent works or speeches, or if the rest is just a matter of interpretation by others.

So from my point of view, you could argue that it's also a valid Dijkstra's.

As to why you might implement it this way: because it will likely be no slower in practice if we only have positive edges, and because it is quicker to write without having to perform additional checks or not-so-standard heap operations.