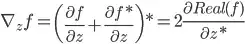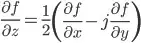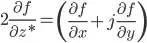5

Let z is a complex variable, C(z) is its conjugation. In complex analysis theory, the derivative of C(z) w.r.t z don't exist. But in tesnsorflow, we can calculate dC(z)/dz and the result is just 1. Here is an example:

x = tf.placeholder('complex64',(2,2))
y = tf.reduce_sum(tf.conj(x))
z = tf.gradients(y,x)
sess = tf.Session()
X = np.random.rand(2,2)+1.j*np.random.rand(2,2)
X = X.astype('complex64')
Z = sess.run(z,{x:X})[0]

The input X is

[[0.17014372+0.71475762j  0.57455420+0.00144318j]
 [0.57871044+0.61303568j  0.48074263+0.7623235j ]]

and the result Z is

[[1.-0.j  1.-0.j]
 [1.-0.j  1.-0.j]]

I don't understand why the gradient is set to be 1? And I want to know how tensorflow handles the complex gradients in general.

zhd.zhang
  • 51
  • 2

2 Answers2

3

How?

The equation used by Tensorflow for the gradient is:

tf-grad-def

Where the '*' means conjugate.

When using the definition of the partial derivatives wrt z and z* it uses Wirtinger Calculus. Wirtinger calculus enables to calculate the derivative wrt a complex variable for non-holomorphic functions. The Wirtinger definition is:

wirtinger

Why this definition?

When using for example Complex-Valued Neural Networks (CVNN) the gradients will be used over non-holomorphic, real-valued scalar function of one or several complex variables, tensorflow definition of a gradient can then be written as:

This definition corresponds with the literature of CVNN like for example chapter 4 section 4.3 of this book or Amin et al. (between countless examples).

J Agustin Barrachina
  • 3,501
  • 1
  • 32
  • 52
2

Bit late, but I came across this issue recently too.

The key point is that TensorFlow defines the "gradient" of a complex-valued function f(z) of a complex variable as "the gradient of the real map F: (x,y) -> Re(f(x+iy)), expressed as a complex number" (the gradient of that real map is a vector in R^2, so we can express it as a complex number in the obvious way).

Presumably the reason for that definition is that in TF one is usually concerned with gradients for the purpose of running gradient descent on a loss function, and in particular for identifying the direction of maximum increase/decrease of that loss function. Using the above definition of gradient means that a complex-valued function of complex variables can be used as a loss function in a standard gradient descent algorithm, and the result will be that the real part of the function gets minimised (which seems to me a somewhat reasonable interpretation of "optimise this complex-valued function").

Now, to your question, an equivalent way to write that definition of gradient is

gradient(f) := dF/dx + idF/dy = conj(df/dz + dconj(f)/dz)

(you can easily verify that using the definition of d/dz). That's how TensorFlow handles complex gradients. As for the case of f(z):=conj(z), we have df/dz=0 (as you mention) and dconj(f)/dz=1, giving gradient(f)=1.

I wrote up a longer explanation here, if you're interested: https://github.com/tensorflow/tensorflow/issues/3348#issuecomment-512101921

Harry Slatyer
  • 21
  • 2