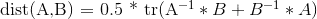Matrix inversion (3,3) python - hard coded vs numpy.linalg.inv

Question

For a large number of matrices i need to compute a distance measure defined as:

Although I do know that matrix inversion is strongly discouraged, I do not see a way around it. Therefore I tried to improve the performance by hard coding the matrix inversion, as all matrices are of size (3,3).

I expected it to be at least a tiny improvement, yet it is not.

Why is numpy.linalg.inv faster/more performant than this hard-coded matrix inversion?

Further, what alternatives do I have to improve this bottleneck?

def inversion(m):    
    m1, m2, m3, m4, m5, m6, m7, m8, m9 = m.flatten()
    determinant = m1*m5*m9 + m4*m8*m3 + m7*m2*m6 - m1*m6*m8 - m3*m5*m7 - m2*m4*m9  
    return np.array([[m5*m9-m6*m8, m3*m8-m2*m9, m2*m6-m3*m5],
                     [m6*m7-m4*m9, m1*m9-m3*m7, m3*m4-m1*m6],
                     [m4*m8-m5*m7, m2*m7-m1*m8, m1*m5-m2*m4]])/determinant

For a timing comparison with a random 3*3 matrix:

%timeit np.linalg.inv(a)

100000 loops, best of 3: 12.5 µs per loop

%timeit inversion(a)

100000 loops, best of 3: 13.9 µs per loop

Closely related yet not at all a duplicate is this post on code-review, which explains the background and the whole function.

EDIT: As @Divakar suggested in the comment, m.ravel() instead of m.flatten() is improving the inversion a little so that the timing comparison now yields:

numpy - 100000 loops, best of 3: 12.6 µs per loop

hard coded - 100000 loops, best of 3: 12.8 µs per loop

Although the gap is closing, the hard coded one is yet slower. How so?

Would you thus conclude that hard-coded python could not be faster than numpy.linalg.inv? — Nikolas Rieble, Feb 27 '17 at 15:33
Store the reciprocal of `determinant` and then use it for multiplications with the (3x3) array? Not sure if you would see any boost here tho. The [`idea`](http://stackoverflow.com/a/41945198/3293881). — Divakar, Feb 27 '17 at 15:34
@NikolasRieble it depends on the case, implementation and numpy's backends. — Eli Korvigo, Feb 27 '17 at 15:34
@Korvigo, could you elaborate or link information? In which case could it be faster? — Nikolas Rieble, Feb 27 '17 at 15:38

Paul Panzer · Accepted Answer · 2017-02-27T18:56:05.347

Here is a humble optimisation, saving 9 multiplications and 3 subtractions

def inversion(m):    
    m1, m2, m3, m4, m5, m6, m7, m8, m9 = m.ravel()
    inv = np.array([[m5*m9-m6*m8, m3*m8-m2*m9, m2*m6-m3*m5],
                    [m6*m7-m4*m9, m1*m9-m3*m7, m3*m4-m1*m6],
                    [m4*m8-m5*m7, m2*m7-m1*m8, m1*m5-m2*m4]])
    return inv / np.dot(inv[0], m[:, 0])

You can squeeze out a few more ops (another 24 multiplications if I'm counting correctly) by doing the entire trace in one go:

def det(m):
   m1, m2, m3, m4, m5, m6, m7, m8, m9 = m.ravel()
   return np.dot(m[:, 0], [m5*m9-m6*m8, m3*m8-m2*m9, m2*m6-m3*m5])
   # or try m1*(m5*m9-m6*m8) + m4*(m3*m8-m2*m9) + m7*(m2*m6-m3*m5)
   # probably the fastest would be to inline the two calls to det
   # I'm not doing it here because of readability but you should try it

def dist(m, n):
   m1, m2, m3, m4, m5, m6, m7, m8, m9 = m.ravel()
   n1, n2, n3, n4, n5, n6, n7, n8, n9 = n.ravel()
   return 0.5 * np.dot(
       m.ravel()/det(m) + n.ravel()/det(n),
       [m5*n9-m6*n8, m6*n7-m4*n9, m4*n8-m5*n7, n3*m8-n2*m9, n1*m9-n3*m7,
        n2*m7-n1*m8, m2*n6-m3*n5, m3*n4-m1*n6, m1*n5-m2*n4])

Ok here is the inlined version:

import numpy as np
from timeit import timeit

def dist(m, n):
   m1, m2, m3, m4, m5, m6, m7, m8, m9 = m.ravel()
   n1, n2, n3, n4, n5, n6, n7, n8, n9 = n.ravel()
   return 0.5 * np.dot(
       m.ravel()/(m1*(m5*m9-m6*m8) + m4*(m3*m8-m2*m9) + m7*(m2*m6-m3*m5))
       + n.ravel()/(n1*(n5*n9-n6*n8) + n4*(n3*n8-n2*n9) + n7*(n2*n6-n3*n5)),
       [m5*n9-m6*n8, m6*n7-m4*n9, m4*n8-m5*n7, n3*m8-n2*m9, n1*m9-n3*m7,
        n2*m7-n1*m8, m2*n6-m3*n5, m3*n4-m1*n6, m1*n5-m2*n4])

def dist_np(m, n):
    return 0.5 * np.diag(np.linalg.inv(m)@n + np.linalg.inv(n)@m).sum()

for i in range(3):
    A, B = np.random.random((2,3,3))
    print(dist(A, B), dist_np(A, B))
    print('pp     ', timeit('f(A,B)', number=10000, globals={'f':dist, 'A':A, 'B':B}))
    print('numpy  ', timeit('f(A,B)', number=10000, globals={'f':dist_np, 'A':A, 'B':B}))

prints:

2.20109953156 2.20109953156
pp      0.13215381593909115
numpy   0.4334693900309503
7.50799877993 7.50799877993
pp      0.13934064202476293
numpy   0.32861811900511384
-0.780284449609 -0.780284449609
pp      0.1258618349675089
numpy   0.3110764700686559

Note that you can make another substantial saving by batch-processing using a vectorised version of the function. The test computes all 10,000 pairwise distances between two batches of 100 matrices:

def dist(m, n):
    m = np.moveaxis(np.reshape(m, m.shape[:-2] + (-1,)), -1, 0)
    n = np.moveaxis(np.reshape(n, n.shape[:-2] + (-1,)), -1, 0)
    m1, m2, m3, m4, m5, m6, m7, m8, m9 = m
    n1, n2, n3, n4, n5, n6, n7, n8, n9 = n
    return 0.5 * np.einsum("i...,i...->...",
        m/(m1*(m5*m9-m6*m8) + m4*(m3*m8-m2*m9) + m7*(m2*m6-m3*m5))
        + n/(n1*(n5*n9-n6*n8) + n4*(n3*n8-n2*n9) + n7*(n2*n6-n3*n5)),
        [m5*n9-m6*n8, m6*n7-m4*n9, m4*n8-m5*n7, n3*m8-n2*m9, n1*m9-n3*m7,
         n2*m7-n1*m8, m2*n6-m3*n5, m3*n4-m1*n6, m1*n5-m2*n4])

def dist_np(m, n):
    return 0.5 * (np.linalg.inv(m)@n + np.linalg.inv(n)@m)[..., np.arange(3), np.arange(3)].sum(axis=-1)

for i in range(3):
    A = np.random.random((100,1,3,3))
    B = np.random.random((1,100,3,3))
    print(np.allclose(dist(A, B), dist_np(A, B)))
    print('pp     ', timeit('f(A,B)', number=100, globals={'f':dist, 'A':A, 'B':B}))
    print('numpy  ', timeit('f(A,B)', number=100, globals={'f':dist_np, 'A':A, 'B':B}))

prints:

True
pp      0.14652886800467968
numpy   1.5294789629988372
True
pp      0.1482033939100802
numpy   1.6455406049499288
True
pp      0.1279512889450416
numpy   1.370200254023075

Although a nice move, it performs worse (=slower) than the version in the question. %timeit np.linalg.inv(a) - 100000 loops, best of 3: 17.2 µs per loop %timeit inversion_paul(a) - 10000 loops, best of 3: 21.2 µs per loop %timeit inversion_niko(a) - 100000 loops, best of 3: 19.2 µs per loop — Nikolas Rieble, Feb 27 '17 at 17:29
@NikolasRieble Have a look at the latest update. In my benchmarks it's a factor 2-3 faster than numpy. — Paul Panzer, Feb 27 '17 at 18:29
@NicolasRIeble Vectorised version gives a 10x speedup over numpy when batch-processing. — Paul Panzer, Feb 27 '17 at 19:01
Impressive improvement. Would you mind to take a look at http://codereview.stackexchange.com/questions/154926/efficient-extraction-of-patch-features-over-an-image and see how i have to extract the matrices from an image. — Nikolas Rieble, Feb 27 '17 at 19:02
@NikolasRieble Assuming you have two lists of 3x3 arrays. (1) convert them to arrays A (mx3x3) B (nx3x3) (2) simply do `A = A[:, None, ...]; B = B[None, ...]` (3) passing these to the vectorised `dist` should return an `mxn` array of distances. -- Extracting the patches to a list either do a list comprehension or allocate an mx3x3 empty array and loop over the 9 pixels using advanced indexing with your coordinate list (adding all combinations of 0, 1, 2 to the two coordinates). — Paul Panzer, Feb 27 '17 at 19:16

avysk · Answer 2 · 2017-02-27T18:29:45.033

I guess there is small overhead of creating four Python objects (four lists) when you call np.array().

I've created the following file (test.py):

import numpy as np

def one():
    return np.array([[0.1,0.2,0.3],[0.4,0.5,0.6],[0.7,0.8,0.9]])

def two():
    a = np.zeros((3, 3))
    a[0,0]=0.1
    a[0,1]=0.2
    a[0,2]=0.3
    a[1,0]=0.4
    a[1,1]=0.5
    a[1,2]=0.6
    a[2,0]=0.7
    a[2,1]=0.8
    a[2,2]=0.9
    return a

Both one() and two() are doing the same thing. However, one() in the process creates four Python lists, and two() does not. Now:

$ python -m timeit -s 'from test import one' 'one()'
100000 loops, best of 3: 3.13 usec per loop
$ python -m timeit -s 'from test import one' 'one()'
100000 loops, best of 3: 2.95 usec per loop
$ python -m timeit -s 'from test import one' 'one()'
100000 loops, best of 3: 3 usec per loop
$ python -m timeit -s 'from test import two' 'two()'
1000000 loops, best of 3: 1.61 usec per loop
$ python -m timeit -s 'from test import two' 'two()'
1000000 loops, best of 3: 1.76 usec per loop
$ python -m timeit -s 'from test import two' 'two()'
1000000 loops, best of 3: 1.69 usec per loop

I've also tried with tuples instead of lists, and the result is as expected (slower than no new Python objects but faster than lists, as tuples are non-modifiable and overhead of those is probably smaller)

def three():
    return np.array(((0.1, 0.2, 0.3),(0.4,0.5,0.6),(0.7,0.8,0.9)))

$ python -m timeit -s 'from test import three' 'three()'
100000 loops, best of 3: 2.11 usec per loop
$ python -m timeit -s 'from test import three' 'three()'
100000 loops, best of 3: 2.03 usec per loop
$ python -m timeit -s 'from test import three' 'three()'
100000 loops, best of 3: 2.08 usec per loop

Although a small improvement compared to the other answer, it adds another perspective! — Nikolas Rieble, Feb 27 '17 at 19:03

Matrix inversion (3,3) python - hard coded vs numpy.linalg.inv

2 Answers2

Linked