Finding if two images are similar

Question

I'm trying to find out it two images are similar with openCV using image matching. I'm running the following code:

public static void match(String firstImage, String secondImage, String outputFile) {

    FeatureDetector detector = FeatureDetector.create(FeatureDetector.ORB);
    DescriptorExtractor descriptor = DescriptorExtractor.create(DescriptorExtractor.ORB);
    DescriptorMatcher matcher = DescriptorMatcher.create(DescriptorMatcher.BRUTEFORCE_HAMMING);


    Mat firstImg = Imgcodecs.imread(firstImage, Imgcodecs.CV_LOAD_IMAGE_GRAYSCALE);
    MatOfKeyPoint firstKeypoints = new MatOfKeyPoint();
    Mat firstDescriptors = new Mat();
    detector.detect(firstImg, firstKeypoints);
    descriptor.compute(firstImg, firstKeypoints, firstDescriptors);

    Mat secondImg = Imgcodecs.imread(secondImage,      Imgcodecs.CV_LOAD_IMAGE_GRAYSCALE);
    MatOfKeyPoint secondKeypoints = new MatOfKeyPoint();
    Mat secondDescriptors = new Mat();
    detector.detect(secondImg, secondKeypoints);
    descriptor.compute(secondImg, secondKeypoints, secondDescriptors);

    MatOfDMatch matches = new MatOfDMatch();
    matcher.match(firstDescriptors, secondDescriptors, matches);

    float minDis = Float.MAX_VALUE;
    for (int i = 0;i < matches.rows();i++) {
        if (matches.toArray()[i].distance < minDis)
            minDis = matches.toArray()[i].distance;
    }
    LinkedList<DMatch> goodMatches = new LinkedList<>();
    for (int i = 0;i < matches.rows();i++) {
        if (matches.toArray()[i].distance < minDis*3)
            goodMatches.add(matches.toArray()[i]);
    }


    List<Point> pts1 = new ArrayList<Point>();
    List<Point> pts2 = new ArrayList<Point>();
    for(int i = 0; i<goodMatches.size(); i++){
        pts1.add(firstKeypoints.toList().get(goodMatches.get(i).queryIdx).pt);
        pts2.add(secondKeypoints.toList().get(goodMatches.get(i).trainIdx).pt);
    }

    // convertion of data types - there is maybe a more beautiful way
    Mat outputMask = new Mat();
    MatOfPoint2f pts1Mat = new MatOfPoint2f();
    pts1Mat.fromList(pts1);
    MatOfPoint2f pts2Mat = new MatOfPoint2f();
    pts2Mat.fromList(pts2);

    Calib3d.findHomography(pts1Mat, pts2Mat, Calib3d.RANSAC, 15, outputMask, 2000, 0.995);

    // outputMask contains zeros and ones indicating which matches are filtered
    LinkedList<DMatch> betterMatches = new LinkedList<DMatch>();
    for (int i = 0; i < goodMatches.size(); i++) {
        if (outputMask.get(i, 0)[0] != 0.0) {
            betterMatches.add(goodMatches.get(i));
        }
    }

    Mat outputImg = new Mat();
    MatOfDMatch betterMatchesMat = new MatOfDMatch();
    betterMatchesMat.fromList(betterMatches);
    Features2d.drawMatches(firstImg, firstKeypoints, secondImg, secondKeypoints, betterMatchesMat, outputImg);
    Imgcodecs.imwrite(outputFile, outputImg);
}

When the images are similar the result looks like:

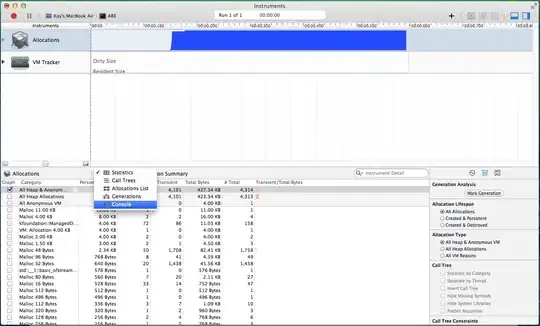
similar example

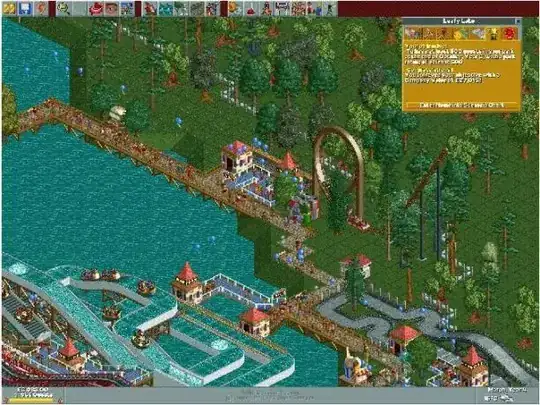
When the images are not similar the result looks like: non similar example

You can see that in the first case the match lines are parallel so it makes sense that the two images are similar. In the second case the match lines are not parallel so it makes sense that the images are not similar. Is there a standard way to analyse these matches and to find in which case the images are most probably similar?

ORB, SIFT, SURF and others are mainly used to find a particular object in an image. You can perform correlation to determine similarity of images. Can you upload the image you are using separately? — Jeru Luke, Feb 28 '17 at 10:32
parallelity isn't enough to tell whether the matching was successful, if you are assuming nearly stationary camera, or a nearly planar scene/object you can compute a homography from the matched points. If a "good" homography is found, the images are quite equal concerning those points. In addition, after "applying" the homography (e.g. image warping) you can compare both images better with simple methods like comparing pixels. All in all the topic is quite hard, but depending on your definition/needs of "image similarity" it might or might not become easier. — Micka, Feb 28 '17 at 10:36
@JeruLuke the source images are: https://i.stack.imgur.com/GH1Qx.jpg https://i.stack.imgur.com/Vfdi8.jpg https://i.stack.imgur.com/qhZEF.jpg — DanielB, Feb 28 '17 at 14:21
@JeruLuke what do you mean by correlation? note that the images are not the same but similar — DanielB, Feb 28 '17 at 14:23
@Micka How can you tell that an homography is "good". is there some kind of a quality score? — DanielB, Feb 28 '17 at 14:25
the number of inliers (and their distribution in the image) is a good hint. Probably there are other criteria, too, like assumptions about maximum scale changes, distortions, etc. — Micka, Feb 28 '17 at 14:29
@Micka maybe you can throw some more light with a detailed explanation in the answering section.....It would be of much help....:) — Jeru Luke, Feb 28 '17 at 17:05
For checking the "good-ness" of homography matrix, see [this](https://stackoverflow.com/questions/14954220/how-to-check-if-obtained-homography-matrix-is-good/41828248) — Rick M., Feb 28 '17 at 17:19

score 3 · Accepted Answer · answered Feb 28 '17 at 17:28

For checking the appropriateness of homography matrix between two perspectives of similar images, I wrote this function. You can choose what you prefer out of the possibilities, depending on which one you find more suitable:

 private static boolean check_homography(Mat homography_mat){
    /* Check 1. Compute the determinant of the homography, and see if it's too close 
     to zero for comfort*/
    if(!homography_mat.empty())
    {
        double Determinant = Core.determinant(homography_mat);
        if (Determinant > 0.1)
            return true;
        else 
            return false;
    }
    else 
        return false;

    /* Check 2. Compute its SVD, and verify that the ratio of the first-to-last 
     singular value is not too high (order of 1.0E7). */   
    Mat singularValues = new Mat();
    Core.SVDecomp(homography_mat, singularValues, new Mat(), new Mat(), Core.SVD_NO_UV);

    System.out.print("\n Printing the singular values of the homography");
    for (int i = 0; i < singularValues.rows(); i++){
        for ( int j = 0; j < singularValues.cols(); j++){
            System.out.print("\n Element at ( " + i + ", " + j + " ) is " + singularValues.get(i, j)[0]);
        }
    }
    double conditionNumber = singularValues.get(0, 0)[0] / singularValues.get(2, 0)[0];
    System.out.print("\n Condition number is : " + conditionNumber);

    if(conditionNumber < Math.pow(10, 7)){
        System.out.print("\n Homography matrix is non-singular");
        return true;
        }
    else{
        System.out.print("\n Homography matrix is singular (or very close)");
        return false;
        }
    /* Check 3. Check the compare absolute values at (0,0) and (0,1) with (1,1) and (1,0) 
     * respectively. If the two differences are close to 0, the homography matrix is 
     * good. (This just takes of rotation and not translation)
     * */
    if(Math.abs((Math.abs(homography_mat.get(0, 0)[0]) - Math.abs(homography_mat.get(1, 1)[0]))) <= 0.1){
        if(Math.abs((Math.abs(homography_mat.get(0, 1)[0]) - Math.abs(homography_mat.get(1, 0)[0]))) <= 0.1){
            System.out.print("\n The homography matrix is good");
            return true;
        }
    }
        else{
            System.out.print("\n The homography matrix is bad");
            return false;
        }
    return false;
    /*
     * Check 4: If the determinant of the top-left 2 by 2 matrix (rotation) > 0, transformation is orientation
     * preserving.
     * Else if the determinant is < 0, it is orientation reversing
     * 
     * */
     Determinant of the rotation mat
    double det = homography_mat.get(0, 0)[0] * homography_mat.get(1,1)[0] - homography_mat.get(0, 1)[0] * homography_mat.get(1, 0)[0];
    if (det < 0)
        return false;

    double N1 = Math.sqrt(homography_mat.get(0, 0)[0] * homography_mat.get(0, 0)[0] + homography_mat.get(1, 0)[0] * homography_mat.get(1, 0)[0]);
    if (N1 > 4 || N1 < 0.1)
        return false;

    double N2 = Math.sqrt(homography_mat.get(0, 1)[0] * homography_mat.get(0, 1)[0] + homography_mat.get(1, 1)[0] * homography_mat.get(1, 1)[0]);
    if (N2 > 4 || N2 < 0.1)
        return false;

    double N3 = Math.sqrt(homography_mat.get(2, 0)[0] * homography_mat.get(2, 0)[0] + homography_mat.get(2,1)[0] * homography_mat.get(2, 1)[0]);
    if (N3 < 0.002)
        return false;

    return true;

}

Note - I coded this for Java, OpenCV when using ORB. I personally (with experience I guess), can look at the Homography matrix and say more or less if its good or not and hence the Check 1. Hope it helps!!

EDIT Additionally, as @Micka mentioned, this is subject to your preference, you can also iterate along the two images pixel by pixel to find the similarity. The method I post here is used to check if the homography is good or not, however, it should be noted that you can get bad homography even when two images are similar depending on the images and the method(pre/post processing, descriptor, detector etc. )

Hope it helps the OP too or at the least is appropriate to the problem! — Rick M., Feb 28 '17 at 17:50

score 0 · Answer 2 · answered Feb 28 '17 at 17:04

0

In layman terms, correlation determines the linear relationship between two variables/data-sets/etc.. The relationship maybe positively linear or negatively linear. Pearson's R is a common method for finding the correlation coefficient between two variables.

The result of Pearson's R lies between -1 and +1.

-1 -> highly non linear to each other
+1 -> highly linear to each other

It is a numerical way of stating how similar or dissimilar two variables are.

In this case, I am assuming the gray scale images to be the two variables. Prior to calculating it I am flattening the image into 1D arrays.

Pearson's R can be determined by using the scipy library (in Python).

from scipy.stats.stats import pearsonr

To get more information about pearsonr and its return type, check THIS LINK

So using python I computed the Pearson's R for all the three images, with each other.

This is what I got:

For the first two images: (0.62908215058685268, 0.0)
For the second and third image: (-0.34523397781005682, 0.0)
For the first and third image: (-0.36356339857880066, 0.0)

Hence we can say that (in numerical/statistical terms) the first two images are somewhat similar (given the fact that one has a handbag and the other doesn't).

If you perform Pearson's R for two same images, you will obtain a result of 1

answered Feb 28 '17 at 17:04

Jeru Luke

20,118
13
80
87

I don't think that this is suitable here – Rick M. Feb 28 '17 at 17:20
@RickM.Why would you say that? – Jeru Luke Feb 28 '17 at 17:35
First, pearson correlation works for normalized data sets. Second, as you can see from your results, the correlation is misleading, for the latter two cases – Rick M. Feb 28 '17 at 17:44
Point well noted :D – Jeru Luke Feb 28 '17 at 17:45
1

Cheers mate! The correlation does make sense to me but statistics has several correlations, which are all subject to conditions and which to use when is the trick ;) – Rick M. Feb 28 '17 at 17:48
1

Something more appropriate is [here](http://stackoverflow.com/questions/13445497/correlation-among-2-images) – Rick M. Feb 28 '17 at 18:09

Finding if two images are similar

2 Answers2

Linked