Ellipsoid equation containing numerous points

Question

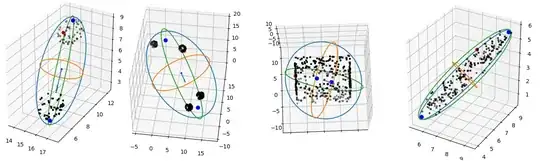
I have a large quantity of pixel colors (96 thousands different colors):

And I want to get some kind of a mathematically-defined probability region like in this question:

The main obstacle I see right now – all methods on Google are mainly about visualisations and about two-dimensional spaces, yet there is no algorithm for finding coefficients of an equation like:

a₁x² + b₁y² + c₁y² + a₂xy + b₂xz + c₂yz + a₃x + b₃y + c₃z = 0

And this paper is too difficult for me to implement it in python. :(

Anyway, what I just want is to determine if some pixel is more-or-less lies within the diapason I have.

I tried making it using scikit clustering, but I failed due to having only one set of data, probably. And creating an array 256³ elements representing each pixel color seems a wrong way.

I wonder if there is an easy way to determine boundaries of this point cluster? Or, maybe I'm just overthinking it and there is something like OpenCV cv2.inRange() function?

Answer 1

this can be solved by optimization and fitting of the ellipsoid polynomial. However I would start with geometrical approach which is much faster:

1. find avg point position

   that will be the center of your ellipsoid

   p0 = sum (p[i]) / n      // average
   i = { 0,1,2,3,...,n-1 }  // of all points
   

   If your point density is not homogenuous then it is safer to use bounding box center instead. So find xmin,ymin,zmin,xmax,ymax,zmax and the middle between them is your center.

2. find most distant point to center

   that will give you main semi axis

   pa = p[j];
   |p[j]-p0| >= |p[i]-p0|   // max
   i = { 0,1,2,3,...,n-1 }  // of all points
   

3. find second semi-axises

   so vector pa-p0 is normal to plane in which the other semi-axises should be. So find most distant point to p0 from that plane:

   pb = p[j];  
   |p[j]-p0| >= |p[i]-p0|   // max
   dot(pa-p0,p[j]-p0) == 0  // but inly if inside plane
   i = { 0,1,2,3,...,n-1 }  // from all points
   

   beware that the result of dot product may not be precisely zero so it is better to test against something like this:

   |dot(pa-p0,p[j]-p0)| <= 1e-3
   

   You can use any threshold you want (should be based on the ellipsoid size).

4. find last semi-axis

   So we know that last semi-axis should be perpendicular to both

   (pa-p0) AND (pb-p0)
   

   So find point such that:

   pc = p[j];  
   |p[j]-p0| >= |p[i]-p0|   // max
   dot(pa-p0,p[j]-p0) == 0  // but inly if inside plane
   dot(pb-p0,p[j]-p0) == 0  // and perpendicular also to b semi-axis
   i = { 0,1,2,3,...,n-1 }  // from all points
   

5. Ellipsoid

   Now you have all the parameters you need to form your ellipsoid. vectors

   (pa-p0),(pb-p0),(pc-p0)
   

   are the basis vectors of your ellipsoid (you can make them perpendicular by using cross product). Their size gives you the radiuses. And p0 is the center. You can also use this parametric equation:

   a=pa-p0;
   b=pb-p0;
   c=pc-p0;
   p(u,v) = p0 + a*cos(u)*cos(v)
               + b*cos(u)*sin(v)
               + c*sin(u);
   u = < -0.5*PI , +0.5*PI >
   v = < 0.0 , 2.0*PI >
   

This whole process is just O(n) and the results can be used as start point for both optimization and fitting to speed them up without the loss of accuracy. If you want to further improve accuracy See:

• How approximation search works

The sub links shows you examples of fitting ...

You can also take a look at this:

• Algorithms: Ellipse matching

which is basically similar to your task but only in 2D still may bring you some ideas.

Answer 2

Here is unstrict solution with fast and simple random search approach*. Best side - no heavy linear algebra library required**. Seems it worked fine for mesh collision detection.

Is assumes that ellipsoid center matches cloud center and then uses some sort of mirrored average to search for main axis.

Full working code is slightly bigger and placed on git, idea of main axis search is here:

np.random.shuffle(pts)

pts_len = len(pts)
pt_average =  np.sum(pts, axis = 0) / pts_len

vec_major = pt_average * 0
minor_max, major_max = 0, 0

# may be improved with overlapped pass, 
for pt_cur in pts:
    vec_cur = pt_cur - pt_average
    proj_len, rej_len = proj_length(vec_cur, vec_major)

    if proj_len < 0:
        vec_cur = -vec_cur
    vec_major += (vec_cur - vec_major) / pts_len

    major_max = max(major_max, abs(proj_len))
    minor_max = max(minor_max, rej_len)

It can be improved/optimized even more at some points. Examples what it will produce:

And full experiment code with plots

*_{i.e. adjusting code lines randomly until they work}
**_{was actually reason to figure out this solution}