n random numbers within parameters

Question

Let's say I have a number, such as 100, and I want to have 5 different random numbers generated, but they all must add up to 100, how would I do that? (preferably in PHP. For math wizards/statisticians, I don't need truly random numbers, but something that looks random).

So this function, would produce something like this:

5, 51, 9, 18, 19 = 100 34, 52, 3, 7, 4 =100

And so forth.

Ideally, something that takes 5, 100 and produces the rest:

generateRandom(100,5)

I asked a similar question some time ago and got a great response: http://stackoverflow.com/questions/2794582/replace-duplicate-values-in-array-with-new-randomly-generated-values — Russell Dias, Nov 23 '10 at 22:55
possible duplicate of [Non biased return a list of n random positive numbers (>=0) so that their sum == total_sum](http://stackoverflow.com/questions/3959021/non-biased-return-a-list-of-n-random-positive-numbers-0-so-that-their-sum) — Jason S, Nov 23 '10 at 22:58

Dr. belisarius · Accepted Answer · 2012-04-30T21:48:22.787

5

a = RandomInteger[{1, 96}]
b = RandomInteger[{1, 97 - a}]
c = RandomInteger[{1, 98 - a - b}]
d = RandomInteger[{1, 99 - a - b - c}]
e = 100 - a - b - c - d

Samples:

{34,25,26,3,12,Sum =,100}

{90,5,1,1,3,Sum =,100}

{29,16,21,9,25,Sum =,100}

{4,13,71,10,2,Sum =,100}

The numbers are no equally distributed, of course.

Edit

Here is a more homogeneous distribution:

a = RandomInteger[{1, 20}];
b = RandomInteger[{1, 40 - a}];
c = RandomInteger[{1, 60 - a - b}];
d = RandomInteger[{1, 80 - a - b - c}];
e = 100 - a - b - c - d;

Output:

{5,33,2,8,52,Sum =,100}
{14,9,50,5,22,Sum =,100}
{3,23,12,34,28,Sum =,100}
{1,16,4,5,74,Sum =,100}
{6,28,6,9,51,Sum =,100}
{11,25,7,1,56,Sum =,100}
{4,34,12,18,32,Sum =,100}
{6,13,25,26,30,Sum =,100}
{8,27,14,5,46,Sum =,100}
{17,13,23,25,22,Sum =,100}

Here are the frequencies for the numbers:

alt text

Edit

Perhaps a better one:

a = Max[#, 1] & /@ Evaluate[RandomInteger[{1, 20}, 5] - 1];
b = 100 - Total@a;
c = Mod[b, 5];
d = (b - c)/ 5;
a = a + d + {c, 0, 0, 0, 0};

Distribution: alt text

Edit

In Mathematica you can easily generate all 5-Tuples that add up 100 as:

IntegerPartitions[100, {5}]

There are 38225 different beasts, without counting permutations

Length@IntegerPartitions[100, {5}]
(* -> 38225 *)

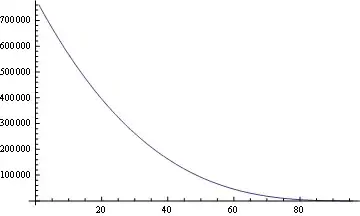
The frequency for each number in those quintuplets is:

Histogram@Flatten@IntegerPartitions[100, {5}]

enter image description here

The curve is very similar if one take permutations into account:

t = Tally@Flatten@(Permutations[#] & /@ IntegerPartitions[100, {5}]); 
ListLinePlot@SortBy[t, #[[1]] &][[All, 2]]

enter image description here

edited Apr 30 '12 at 21:48

answered Nov 23 '10 at 23:11

Dr. belisarius

60,527
15
115
190

Above and beyond, kudos to you. I'm giving you +1 just for effort alone. – Brad Christie Nov 23 '10 at 23:28
@Brad Christie Tip o'the hat :D – Dr. belisarius Nov 23 '10 at 23:31
So, I'm trying to make this in to a function yet rand of 1, in the rand() function of php still gives me a 0 result--strange. otherwise, my updated function works fine, Any ideas on that? I'm thinking of even (rand(1,65535) % $high_value + 1) – Brad Christie Nov 23 '10 at 23:48
@Brad rand(min,max) does not return 0 in php . See here http://ideone.com/clone/2ApUi – Dr. belisarius Nov 23 '10 at 23:56
Touché, I had a mod in there. I thinks that's my queue to get off the computer. ;p Cool site though, found out about a PHP one now instead of just jsfiddle. ;-) – Brad Christie Nov 24 '10 at 00:13
@Brad That was my first line in php :) – Dr. belisarius Nov 24 '10 at 00:15

Brad Christie · Answer 2 · 2010-11-29T14:39:06.333

Along the lines of belisarius:

  // Generates an array (of $elements elements) full of random numbers whose
  // total is equal to the $total_sum
  function generate_random_array($elements = 5, $total_sum = 100)
  {
    // build result array
    $result = Array();

    // iterate over all elements (except for the last, last will be the delta)
    for ($_ = 0; $_ < ($elements - 1); $_++)
    {
      // typical low value (non-zero)
      $low_value = 1;

      // high value, skewed to have high results first
      //$high_value = ($total_sum - ($elements - $_) - array_sum($result));
      // high value, non-skewed
      $step = (int)floor($total_sum / $elements); // give "not-to-exceed" ranges
      $high_value = (($_ + 1) * $step) - array_sum($result);

      // produce the result and add it
      $result[] = rand($low_value,$high_value);
      //$result[] = rand(1,65535) % $high_value + 1; // alternate to make rand a little smoother
    }

    // add the final result as the remainder
    $result[] = $total_sum - array_sum($result);

    // now return it
    return $result;
  }

Almost? Hah, what am I missing? -- You mean your latest update? — Brad Christie, Nov 24 '10 at 00:23

n random numbers within parameters

2 Answers2