Fitting (a gaussian) with Scipy vs. ROOT et al

Question

I have now multiple times stumbled upon that fitting in python with scipy.curve_fit is somehow a lot harder than with other tools like e.g. ROOT (https://root.cern.ch/)

For example, when fitting a gaussian, with scipy I mostly get a straight line:

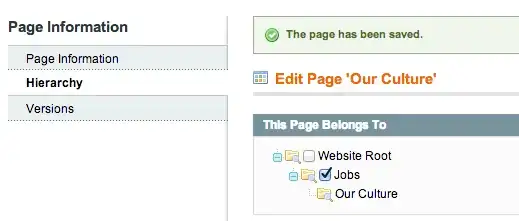
corresponding code:

def fit_gauss(y, x = None):
    n = len(y)  # the number of data
    if x is None:
       x = np.arange(0,n,1)
    mean = y.mean()
    sigma = y.std()

    def gauss(x, a, x0, sigma):
        return a * np.exp(-(x - x0) ** 2 / (2 * sigma ** 2))

    popt, pcov = curve_fit(gauss, x, y, p0=[max(y), mean, sigma])

    plt.plot(x, y, 'b+:', label='data')
    plt.plot(x, gauss(x, *popt), 'ro:', label='fit')
    plt.legend()
    plt.title('Gauss fit for spot')
    plt.xlabel('Pixel (px)')
    plt.ylabel('Intensity (a.u.)')
    plt.show()

Using ROOT, I get a perfect fit, without even giving start parameters:

Again, the corresponding code:

import ROOT
import numpy as np

y = np.array([2., 2., 11., 0., 5., 7., 18., 12., 19., 20., 36., 11., 21., 8., 13., 14., 8., 3., 21., 0., 24., 0., 12., 0., 8., 11., 18., 0., 9., 21., 17., 21., 28., 36., 51., 36., 47., 69., 78., 73., 52., 81., 96., 71., 92., 70., 84.,72., 88., 82., 106., 101., 88., 74., 94., 80., 83., 70., 78., 85., 85., 56., 59., 56., 73., 33., 49., 50., 40., 22., 37., 26., 6., 11., 7., 26., 0., 3., 0., 0., 0., 0., 0., 3., 9., 0., 31., 0., 11., 0., 8., 0., 9., 18.,9., 14., 0., 0., 6., 0.])
x = np.arange(0,len(y),1)
#yerr= np.array([0.1,0.2,0.1,0.2,0.2])
graph = ROOT.TGraphErrors()
for i in range(len(y)):
    graph.SetPoint(i, x[i], y[i])
    #graph.SetPointError(i, yerr[i], yerr[i])
func = ROOT.TF1("Name", "gaus")
graph.Fit(func)

canvas = ROOT.TCanvas("name", "title", 1024, 768)
graph.GetXaxis().SetTitle("x") # set x-axis title
graph.GetYaxis().SetTitle("y") # set y-axis title
graph.Draw("AP")

Can someone explain to me, why the results differ that much? Is the implementation in scipy that bad / dependend on good start parameters? Is there any way around it? I need to process a lot of fits automatically, but don't have access to ROOT on the target computer, so it has to work with python only.

When taking the results from the ROOT fit and giving them to scipy as the start parameters, the fit works fine with scipy as well...

Answer 1

Without actual data it is not that easy to reproduce your results but with artificially created noisy data it looks fine to me:

That is the code I am using:

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# your gauss function
def gauss(x, a, x0, sigma):
    return a * np.exp(-(x - x0) ** 2 / (2 * sigma ** 2))

# create some noisy data
xdata = np.linspace(0, 4, 50)
y = gauss(xdata, 2.5, 1.3, 0.5)
y_noise = 0.4 * np.random.normal(size=xdata.size)
ydata = y + y_noise
# plot the noisy data
plt.plot(xdata, ydata, 'bo', label='data')

# do the curve fit using your idea for the initial guess
popt, pcov = curve_fit(gauss, xdata, ydata, p0=[ydata.max(), ydata.mean(), ydata.std()])

# plot the fit as well
plt.plot(xdata, gauss(xdata, *popt), 'r-', label='fit')

plt.show()

As you, I also use p0=[ydata.max(), ydata.mean(), ydata.std()] as an initial guess and that seems to work fine and robust for different noise strengths.

EDIT

I just realized that you actually provide data; then the result looks as follows:

Code:

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit


def gauss(x, a, x0, sigma):
    return a * np.exp(-(x - x0) ** 2 / (2 * sigma ** 2))

ydata = np.array([2., 2., 11., 0., 5., 7., 18., 12., 19., 20., 36., 11., 21., 8., 13., 14., 8., 3., 21., 0., 24., 0., 12.,
0., 8., 11., 18., 0., 9., 21., 17., 21., 28., 36., 51., 36., 47., 69., 78., 73., 52., 81., 96., 71., 92., 70., 84.,72.,
88., 82., 106., 101., 88., 74., 94., 80., 83., 70., 78., 85., 85., 56., 59., 56., 73., 33., 49., 50., 40., 22., 37., 26.,
6., 11., 7., 26., 0., 3., 0., 0., 0., 0., 0., 3., 9., 0., 31., 0., 11., 0., 8., 0., 9., 18.,9., 14., 0., 0., 6., 0.])

xdata = np.arange(0, len(ydata), 1)

plt.plot(xdata, ydata, 'bo', label='data')

popt, pcov = curve_fit(gauss, xdata, ydata, p0=[ydata.max(), ydata.mean(), ydata.std()])
plt.plot(xdata, gauss(xdata, *popt), 'r-', label='fit')

plt.show()

Answer 2

You may not have really wanted to use ydata.mean() for the initial value of the Gaussian centroid, or ydata.std() for the initial value of the variance -- those are probably better guessed from xdata. I don't know if that is what caused the initial trouble.

You might find the lmfit library useful. This provides a way to turn your model function gauss into a Model class with a fit() method that uses named Parameters determined from your model function. Using it, your fit might look like:

import numpy as np
import matplotlib.pyplot as plt

from lmfit import Model

def gauss(x, a, x0, sigma):
    return a * np.exp(-(x - x0) ** 2 / (2 * sigma ** 2))

ydata = np.array([2., 2., 11., 0., 5., 7., 18., 12., 19., 20., 36., 11., 21., 8., 13., 14., 8., 3., 21., 0., 24., 0., 12., 0., 8., 11., 18., 0., 9., 21., 17., 21., 28., 36., 51., 36., 47., 69., 78., 73., 52., 81., 96., 71., 92., 70., 84.,72., 88., 82., 106., 101., 88., 74., 94., 80., 83., 70., 78., 85., 85., 56., 59., 56., 73., 33., 49., 50., 40., 22., 37., 26., 6., 11., 7., 26., 0., 3., 0., 0., 0., 0., 0., 3., 9., 0., 31., 0., 11., 0., 8., 0., 9., 18.,9., 14., 0., 0., 6., 0.])

xdata = np.arange(0, len(ydata), 1)

# wrap your gauss function into a Model
gmodel = Model(gauss)
result = gmodel.fit(ydata, x=xdata, 
                    a=ydata.max(), x0=xdata.mean(), sigma=xdata.std())

print(result.fit_report())

plt.plot(xdata, ydata, 'bo', label='data')
plt.plot(xdata, result.best_fit, 'r-', label='fit')
plt.show()

There are several additional features. For example, you might want to see the confidence in the best fit, which would be (in master version, soon-to-be-released):

# add estimated band of uncertainty:
dely = result.eval_uncertainty(sigma=3)
plt.fill_between(xdata, result.best_fit-dely, result.best_fit+dely, color="#ABABAB")
plt.show()

to give: