Get best linear function which approximate some dots in 3D

Question

I have 4 dots which are represented with these coordinates:

X = [0.1, 0.5, 0.9, 0.18]
Y = [0.7, 0.5, 0.7, 0.3]
Z = [4.2, 3.3, 4.2, 2.5]

and I have to get the best linear function (plane) which approximate these 4 dots.

I'm aware of numpy.polyfit, but polyfitworks only with x and y (2D), What can I do?

@BillBell Z is simply a list with the coordinates of my 4 dots in the Z axis, not a function. — Patricio Sard, Mar 16 '17 at 18:12
Not what I meant. You want a line. There are various ways of fitting such a line. One way is to write Z = aX + bY + error, then estimate a and b. Another is to calculate the eigenvectors of the variance-covariance matrix of X, Y and Z. The first way can be extended to allow polynomial functions of X, Y and Z. Is this what you want? — Bill Bell, Mar 16 '17 at 18:15
@BillBell Sorry, my mistake, it has to be a linear function, i.e. a plane, for example `ax + by + cz = d` — Patricio Sard, Mar 16 '17 at 18:23
http://stackoverflow.com/questions/1400213/3d-least-squares-plane seems to be what you want. — Bill Bell, Mar 16 '17 at 19:16

f5r5e5d · Answer 1 · 2017-03-16T22:48:20.747

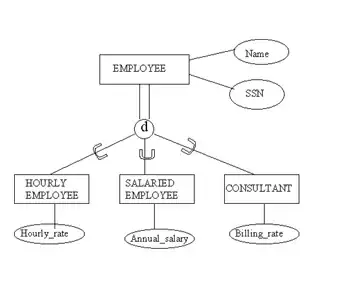
while not completely general, if the the data points can be reasonably represented as a surface relative to a coordinate plane, say z = ax + by + c then np.linalg.lstsq can be used

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np

X = np.array([0.1, 0.5, 0.9, 0.18])
Y = np.array([0.7, 0.5, 0.7, 0.3])
Z = np.array([4.2, 3.3, 4.2, 2.5])

# least squares fit
A = np.vstack([X, Y, np.ones(len(X))]).T

a,b,c=  np.linalg.lstsq(A, Z)[0]

# plots

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# plot data as big red crosses
ax.scatter(X, Y, Z, color='r', marker='+', linewidth=10)

# plot plane fit as grid of green dots

xs = np.linspace(min(X), max(X), 10)
ys = np.linspace(min(Y), max(Y), 10)
xv, yv = np.meshgrid(xs, ys)
zv = a*xv + b*yv + c

ax.scatter(xv, yv, zv, color = 'g')
# ax.plot_wireframe(xv, yv, zv, color = 'g') # alternative fit plane plot
plt.show()

plotting the data 1st, you could select a different coordinate pair for the "independent variable" plane to avoid ill conditioned result if necessary, if the data points appeared to lie in a plane containing the z axis, then use xz or yz

and of course you could have degenerate points on a line or the vertices of a regular tetrahedron

for a better "geometric fit" the 1st fitted plane could be used as the base for a 2nd least square fit of the data rotated into that coordinate system (if the data is "reasonably" plane like)

Get best linear function which approximate some dots in 3D

1 Answers1