Algorithm complexity Min and max

Question

I have a question..I got an algorithm

procedure summation(A[1...n])
s=0
for i= 1 to n do
     j=min{max{i,A[i],n^3}
     s= s + j
return s

And I want to find the min and max output at this algorithm with the use of asymptotic notation θ. Any ideas on how to do that? What I have to look on an algorithm to understand it's complexity?

Possible duplicate of [Algorithm asymptotic-complexity](http://stackoverflow.com/questions/42816454/algorithm-asymptotic-complexity) — Paul Hankin, Mar 26 '17 at 18:13

score 2 · Answer 1 · edited May 23 '17 at 12:25

If you want to know the big O notation or time complexity works? You might want to look at the following post What is a plain English explanation of "Big O" notation?.

For the psuedo code that you showed, the complexity is O(n). were n is the length of the array. Often you can determine the complexity by just looking at how many nested loops the algorithm has. Of course is this not always the case but this can used as rule of thumb.

In the following example:

procedure summation(A[B1[1...n],B2[1...n],...,Bn[1...n]])
s=0
for i= 1 to n do
    for j= 1 to m do
     j=min{max{i,A[i,j],n^3}
     s= s + j
return s

the complexity would be O(n m). (length of all arrays b -> m)

best or worst case

For the algorithm that you showed there is no best or worse case. It always runs the same time for the same array, the only influence on the run time is the length of the array.

An example where there you could be a best or worst case is following. lets say you need to find the location of a specific number in a array. If you method would be to to through the array from start to end. The best case would that the number is at the start. The worst case would be if the number would be at the end.

For a more detailed explanation look at the link. Cheers.

Thank you so so soo much!! I almost understand everything from your post!! Also the link was so usefull ! You are the best ! Thanks and have a nice day! — Mikel, Mar 23 '17 at 16:10
@Mikel Shit, you did not ask about the time complexity of the algoritm. The correct answer is geven below. — Gijs Den Hollander, Mar 23 '17 at 21:58

Paraskevas Leivadaros · Accepted Answer · 2018-01-07T12:15:57.510

The best and the worst case are the same because the algorithm will run the "same way" every time no matter the input. So based on that we will calculate the time complexity of the algorithm using math:

T(n) = 1 + (3+2) + 1
T(n) = 2 + 5
T(n) = 2 + 5 1
T(n) = 2 + 5 (n-1+1)
T(n) = 5n + 2

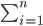This summation formula (3+2) is due to the fact that inside the loop we have 5 distinct and measurable actions:
j = min{max{i,A[i]}, n^3} that counts as three actions because we have 2 comparisons and a value assignment to the variable j.
s = s + j that counts as 2 actions because we have one addition and a value assignment to the variable s.

Asymptotically: Θ(n)

How we calculate Θ(n):
We look at the result that is 5n + 2 and we take out the constants so it becomes n. Then we choose the "biggest" variable that is n.
Other examples:

8n^3+5n+2 -> Θ(n)=n^3
10logn+n^4+7 -> Θ(n)=n^4

More info: http://bigocheatsheet.com/

The loop isnt (1+1)*n = 2n ? Also can u explain me why at 4th line its n? — Mikel, Mar 24 '17 at 13:31
The loop is 2(n+1) because the loop will go on for 1 to n+1 since it will run one more time from n when the i becomes n+1. When this happens the check will be false thus ending the loop. The 4th line is n because the summation will happen n times. — Paraskevas Leivadaros, Jan 06 '18 at 15:00

Algorithm complexity Min and max

2 Answers2