9

How can I identify and remove those four RED points drawn in image alt text

Those four points make that polygon a concave polygon that’s why I want to remove it.

My goal is to convert concave polygon to convex by removing this kind of point by identifying and removing those points.

Is there any way to identify and remove these kind of points?

aioobe
  • 413,195
  • 112
  • 811
  • 826
Pritesh
  • 3,208
  • 9
  • 51
  • 70

4 Answers4

12

Use a convex hull algorithm (such as the Graham scan), and remove all points that are not part of the resulting convex hull.

In your example, the convex hull will consist of P1, P2, P3, P5, P7, P8, P9, P11, P12, P13, P14, P15, P16, P18, which are precisely all points except the red ones.

Note that simply removing those points whose inner angle is greater than 180 will not necessarily result in a convex polygon. Take this polygon for example:

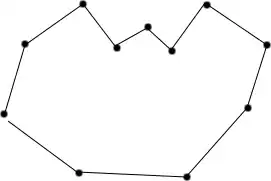
enter image description here

aioobe
  • 413,195
  • 112
  • 811
  • 826
  • 1
    Here's something I've never considered: if you keep removing reflex points for as long as there are any, you must surely end up with a convex polygon? So in the picture above you'd remove the two reflexes, that'd make the one that's between them reflex so then you'd kill it too. I guess a formal proof would depend on proving that such a thing would terminate sensibly. – Tommy Dec 01 '10 at 12:57
  • 1
    Sure, but you'll end up with an n-square algorithm, and as opposed to the Graham Scan, it requires you to know the order of the points. – aioobe Dec 01 '10 at 13:00
3

aioobe has it right—you sound as though you are looking to compute the convex hull of your polygon, in which case you want one of the convex hull algorithms like Graham scan or Chan's algorithm.

However, if you just want to know whether an angle is convex or concave there's a quick way to compute this that avoids trigonometry.

If A, B, and C are consecutive vertices going clockwise around the polygon, then the vertex at B is convex if

(B − A)⟂ · (C − B) < 0

Here V⟂ is a vector that's V rotated by 90° anti-clockwise, which can be computed like so: (x, y)⟂ = (−y, x).

Gareth Rees
  • 64,967
  • 9
  • 133
  • 163
  • here dot(.) means dot product or Multiplication? – Pritesh Dec 01 '10 at 12:07
  • 1
    Dot product. ("Multiplication" almost never makes sense as a vector operation, so vector products with dots may safely be assumed to be dot products.) – Gareth Rees Dec 01 '10 at 12:27
  • Please Check this is Right Calculation. If, A(7, 11) B(8, 9) C(11,8) Then, (B-A)·(C-B) =((8-7,9-11)·(11-8,8-9)) = (1, -2)·(3, -1) = 3 + 2 = 5 > 0, Means point B is Concave. IS IT RIGHT? – Pritesh Dec 01 '10 at 13:58
  • What if A, B and C go counter-clockwise? `<` is just changed to `>` then? – gvlasov May 28 '14 at 18:06
2

You can detect concave points by looking at the interior angle — if it's greater than a half circle then the point is concave. Indeed they're usually called reflex points because the interior angle is reflex.

A quick way to check is the dot product. For example, look at the three points P14, P15, P16. P16 is behind the line that the segment between P14 to P15 lies on (ie, the dot product of the vector from P15 to P16 with the normal to that line is negative), so P15 is a convex point.

P18 is in front of the line that the segment from P16 to P16 lies on (ie, the dot product of the vector from P17 to P18 with the normal of that line is positive), so P17 is a reflex point.

In 2d, the normal of the line is as simple as flipping the x and y coordinates and negating one.

However, what I think you might want is the convex hull — consider whether there might be convex points that nonetheless create a concave hull. The most obvious example is if I left P17 where it is but moved P18 and P16 even further into the shape, behind it. If so then you want to check out convex hull algorithms.

Tommy
  • 99,986
  • 12
  • 185
  • 204
  • 1
    Note that removing points with an inner angle greater than 180 will not necessarily yield a convex polygon. See my answer. – aioobe Dec 01 '10 at 11:17
  • 1
    Oh, yes, I absolutely agree. That's what my final paragraph is meant to say. Please forgive me if I've been ambiguous. – Tommy Dec 01 '10 at 11:18
  • 1
    thanks to your idea I found something interesting. I compare the signed area of the polygon and the signed area of the triangle [prev, point, next], if they have the same sign, the point is "convex" (not reflex). – nraynaud Jan 06 '14 at 03:09
0

I am guessing you have the coordinates for the points (P1, P2, etc.). You can get the angle generated between each three points and remove it if it is less than 180. For figuring out the angle, check How to calculate an angle from three points?

Community
  • 1
  • 1
pinaki
  • 5,393
  • 2
  • 24
  • 32
  • 1
    Note that removing points with an inner angle greater than 180 will not necessarily yield a convex polygon. See my answer. – aioobe Dec 01 '10 at 11:16
  • Hi pinaki, output of angle between three point is always <=180. think about this point. – Pritesh Dec 01 '10 at 12:46