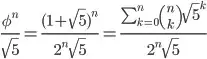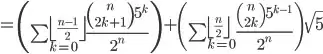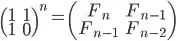I was sent this nice non-recursive function for computing a fibonacci sequence.
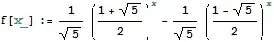
So I coded up a bit of c# and was able to verify all numbers up to 1474 were correct.
The problem comes in when attempting to calculate it for 1475 and above. My c# math skills just aren't up to the task of figuring out a different way. So, does someone have a better way of expressing this particular math function in c#? other than the traditional way of doing a recursive function?
Incidentally, I started to use BigInteger as the return type. But the problem really comes in when trying to raise (1+Math.Sqrt(5) /2) to the 1475th power. I just don't see what data type I need (nor mechanism for that matter) to get this to come back with something other than Infinity.
Here's a starting point.
private Double FibSequence(Int32 input) {
Double part1 = (1 / Math.Sqrt(5));
Double part2 = Math.Pow(((1 + Math.Sqrt(5)) / 2), input);
Double part3 = Math.Pow(((1 - Math.Sqrt(5)) / 2), input);
return (part1 * part2) - (part1 * part3);
}
And, no, it's not homework. Just a "simple" problem for a slow day.
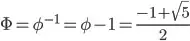 is less than one, so
is less than one, so 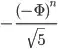 does the same as rounding to the nearest integer, thus you can simplify your solution to finding
does the same as rounding to the nearest integer, thus you can simplify your solution to finding 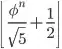 . Then use binomial expansion so that you only have to calculate
. Then use binomial expansion so that you only have to calculate 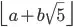 , with appropriate a and b (which are rational and can be computed exactly with BigInteger). If you still go back to Double for this, you still won't get much further than 1475, but you should be able to figure out how to do even this part with exact integer math only ☺
, with appropriate a and b (which are rational and can be computed exactly with BigInteger). If you still go back to Double for this, you still won't get much further than 1475, but you should be able to figure out how to do even this part with exact integer math only ☺