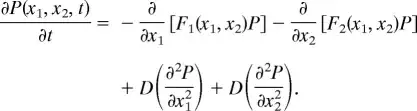I'm attempting to follow some psuedo code for solving cubic equations in Mathematics and Physics for Programmers, Chapter 3, as far as I can see I've followed it accurately, but I don't seem to be getting correct outputs.
For example: According to Wolfram Alpha 5x^3 + 4x^2 + 3x + 2 = 0 should give a root of x≈-0.72932, but I'm getting back -1.8580943294965526 from my script.
Can someone help me to work out what the hell I'm doing? I'm following the scripts to get a better understanding of maths and converting equations to code. But this is at the brink of my understanding so I'm finding it troublesome to debug. Coupled with the fact the book has no errata and many online reviews state the book has many errors, I'm struggling to see whether the issue is with my code, the books explanation or both.
The equation given in the book is:
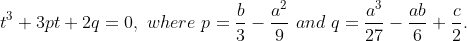
Then if the discriminant > 0 then root has value of r+s:
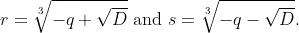
if discriminant == 0 then there are two roots:
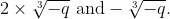
if discriminant < 0 you can find three roots as follows:
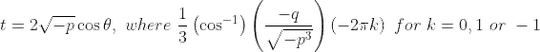
After finding t you can transform it to x by taking:
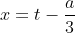
package com.oacc.maths;
public class SolveCubic {
public static double[] solveCubic(double a, double b, double c, double d) {
double[] result;
if (d != 1) {
a = a / d;
b = b / d;
c = c / d;
}
double p = b / 3 - a * a / 9;
double q = a * a * a / 27 - a * b / 6 + c / 2;
double D = p * p * p + q * q;
if (Double.compare(D, 0) >= 0) {
if (Double.compare(D, 0) == 0) {
double r = Math.cbrt(-q);
result = new double[2];
result[0] = 2 * r;
result[1] = -r;
} else {
double r = Math.cbrt(-q + Math.sqrt(D));
double s = Math.cbrt(-q - Math.sqrt(D));
result = new double[1];
result[0] = r + s;
}
} else {
double ang = Math.acos(-q / Math.sqrt(-p * p * p));
double r = 2 * Math.sqrt(-p);
result = new double[3];
for (int k = -1; k <= 1; k++) {
double theta = (ang - 2 * Math.PI * k) / 3;
result[k + 1] = r * Math.cos(theta);
}
}
for (int i = 0; i < result.length; i++) {
result[i] = result[i] - a / 3;
}
return result;
}
public static double[] solveCubic(double a, double b, double c) {
double d = 1;
return solveCubic(a, b, c, d);
}
public static void main(String args[]) {
double[] result = solveCubic(5, 4, 3, 2);
for (double aResult : result) {
System.out.println(aResult);
}
}
}
I also found this code example from the book site(n.b. this is not the psuedo code from the book): http://www.delmarlearning.com/companions/content/1435457331/files/index.asp?isbn=1435457331
on solveCubic(a,b,c,d)
--! ARGUMENTS:
a, b, c, d (all numbers). d is optional (default is 1)
--!
RETURNS: the list of solutions to dx^3+ax^2+bx+c=0
-- if d is defined then divide a, b and c by d
if not voidp(d)
then
if d=0 then return solveQuadratic(b,c,a)
set d to float(d)
set a to a/d
set b to b/d
set
c to c/d
else
set a to float(a)
set b to float(b)
set c to float(c)
end if
set p to b/3 - a*a/9
set q to a*a*a/27 - a*b/6 + c/2
set disc to p*p*p + q*q
if abs(disc)<0.001 then
set r to cuberoot(-q)
set ret to [2*r, -r]
else if disc>0 then
set r to cuberoot(-q+sqrt(disc))
set s to cuberoot(-q-sqrt(disc))
set ret to [r+s]
else
set ang to acos(-q/sqrt(-p*p*p))
set r to 2*sqrt(-p)
set ret to []
repeat with k=-1 to 1
set theta
to (ang - 2*pi*k)/3
ret.add(r*cos(theta))
end repeat
end if
set ret to ret-a/3 --NB: this adds the value to each
element
return ret
end