So, I have tried to solve some big o questions and I had some troubles with some of them. I don't quite understand them.
like for eg the dominant term of 10MlogM + (N/2) log (N/2) + N/4
and M log (N) + M log (M ). I have trouble understanding big o expressions with 'log' in them. Any help would be appreciated and thanks in advance.
- 6,493
- 3
- 30
- 40
- 19
- 1
- 1
- 3
-
2Possible duplicate of [What is a plain English explanation of "Big O" notation?](http://stackoverflow.com/questions/487258/what-is-a-plain-english-explanation-of-big-o-notation) – Paul Hankin Apr 30 '17 at 00:30
-
What are `M` and `N`? Typically, such notation is conventional for graph problems, where `N` and `M` represent the number of vertices and edges, respectively. Technically, `M = O(N^2)`, and the entire thing could be written in terms of `N` alone, but using a separate variable `M` lets you emphasize the part that depends on how dense or sparse the graph is. For example, in a sparse graph, `M log (N) + M log M` might be `N log N`, while in a dense graph it would be closer to `N^2 log N`. – chepner Apr 30 '17 at 00:54
-
This almost feels like it should be ported to a sister site. – Ungeheuer Apr 30 '17 at 03:48
1 Answers
I have trouble understanding big o expressions with 'log' in them
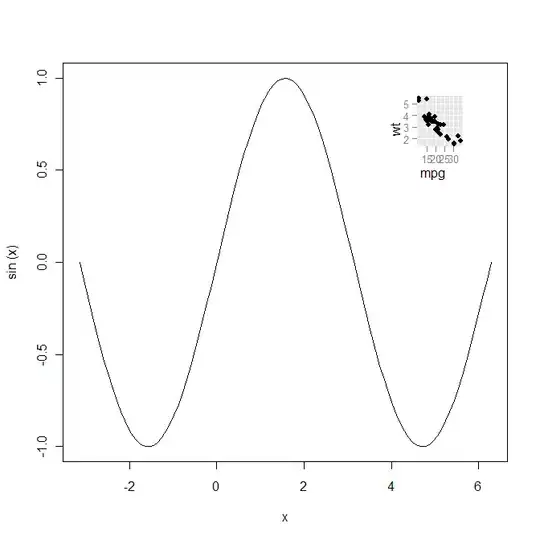
It's quite easy to understand Big-O of log (or any function) if we draw its graph:
Now since you are facing an equation having multiple terms (and one of them is log), so maybe it would confuse you out. If we plot first term (I assume its NlogN and discard the constant (10)):
Similarly for other term (N/2 * log(N/2)):
I am sure you will already know, but this graph easily demonstrates that only major term (N logN) defines the Big O (as its just to show the upper bound of function) as I plot the graph of whole function:
What does N log N mean
This link provides very good explanation with this example:
O(n log n): There was a mix-up at the printer's office, and our phone book had all its pages inserted in a random order. Fix the ordering so that it's correct by looking at the first name on each page and then putting that page in the appropriate spot in a new, empty phone book.
For the below examples, we're now at the printer's office. Phone books are waiting to be mailed to each resident or business, and there's a sticker on each phone book identifying where it should be mailed to. Every person or business gets one phone book.
O(n log n): We want to personalize the phone book, so we're going to find each person or business's name in their designated copy, then circle their name in the book and write a short thank-you note for their patronage.
- 1,977
- 3
- 29
- 48