How to build an and-or tree?

Question

I need a tree structure that supports "and" and "or"ing. For example, given a regular expression like ab|c(d|e) I want to turn that into a tree.

So, at first we have two "or" branches... it can either go down ab, or c(d|e). If you head down the ab branch, you get two nodes, a and b (or a followed by b, whatever). Then if you go down the c(d|e) branch, you get c and (d|e), then (d|e) is split into d or e.

Making a tree structure is easy, you just have something like

class Node {
    string element;
    Node[] children;
}

But then how do you know if the children should be "anded" or "ored"? I guess each level of the tree should alternate between "anding" and "oring"

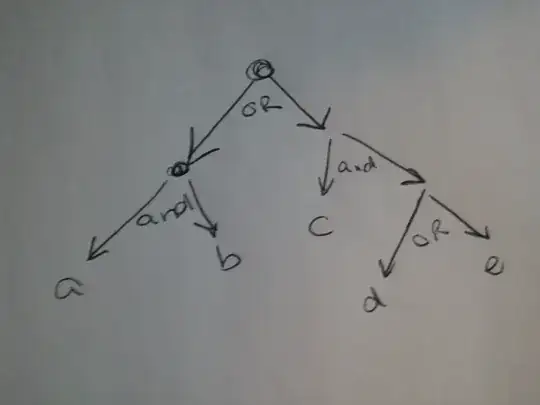
Does that make sense? Can anyone suggest a structure for this?

---

A few people have suggested storing the "operator" on the node, which is fine, but isn't there a way to take advantage of the fact that each level always alternates or,and,or,and,...?

Edit: Not quite sure why people keep assuming this is a binary tree. It's not. I was hoping the tiny code snippet would tip you off. The example just happens to have only 2 branches.

---

Currently leaning towards this:

abstract class Node { }

class DataNode : Node
{
    string data;
}

abstract class OpNode : Node
{
    Node[] children;
}

class OrNode : OpNode { }
class AndNode : OpNode { }

Answer 1

Think of a tree structure where every node represents a boolean expression that can be evaluated to be either true or false - in your case a regular expression (match or non-match). The tree structure itself represents AND and OR: Each route, starting at the root node and ending with a node that has no further children, is a conjunction of expressions, representing AND. The tree

    A
   /
  B
 /
C

would represent A AND B AND C.

Whenever a node has more than 1 child node, there is an OR (disjunction), branching into several routes:

    A
   / \
  B   D
 /
C

represents A AND ((B AND C) OR D)

So you do not even need to store the operators anywhere.

In your example you have the expression ab|c(d|e) so there is no common root expression to evaluate; I suggest the root in this case is simply true and the tree would look like:

   true
   / \
  A   C
 /   / \
B   D   E

For a custom tree class in c# look here Tree data structure in C# or search on or make one of your own.

Answer 2

abstract class Node { }

class DataNode : Node {
    public string Data { get; }

    // details
}

class OperatorNode : Node {
    public Node Left { get; }
    public Node Right { get; }
    public BinaryOperator Operator { get; }

    // details
}

abstract class BinaryOperator { // details }

class Or : BinaryOperator { // details }
class And : BinaryOperator { // details }

Answer 3

You could have 2 types of nodes: operator nodes and variable nodes.

The leaves of your tree would all be variable nodes; all other nodes would be operator nodes.

Binary operator nodes would have two children. Unary operator (like NOT) nodes would have 1 child.

For your example ab|c(d|e):

      OR
  /         \
 AND       AND
 / \      /  \
a   b    c   OR
           /  \
          d    e

Answer 4

Is there anything wrong with this:

enum Operation
{
    None,
    And,
    Or
}

class Node {
    string element;
    Node[] children;
    Operation operation;
}

Edit:

As an example of how ab|c(d|e) would look something like this:

Node root = new Node
        {
            operation = Operation.Or,
            children = new Node[]
            {
                new Node
                {
                    operation = Operation.And,
                    children = new Node[]
                    {
                          new Node{ element = "a" },
                          new Node{ element="b" }
                    }
                },
                new Node
                {
                    children = new Node[]
                    {
                        new Node{ element = "c"},
                        new Node
                        {
                            operation= Operation.Or,
                            children = new Node[]
                            {
                                new Node{ element= "d"},
                                new Node{element = "e"}
                            }
                        }
                    }
                }
            }
        };

Answer 5

I did this just a few days ago using ANTLR. ANTLR provided me with a grammar which is represented as an AST Abstract Syntax Tree as you just described and it generated c# code that could handle that grammar.

It's quite nice and elegant. Here are a few example.

Answer 6

Just to throw in a slightly different one

interface Node
{
    // top level operations here
}

class OpNode : Node
{
    public Node Left { get; set; }
    public Node Right { get; set; }
}

class AndNode : OpNode
{
    public AndNode(Node left, Node right)
    {
        Left = left;
        Right = right;
    }
    public override string ToString()
    {
        return "(" + Left.ToString() + " & " + Right.ToString() + ")";
    }
}

class OrNode : OpNode
{
    public OrNode(Node left, Node right)
    {
        Left = left;
        Right = right;
    }
    public override string ToString()
    {
        return "(" + Left.ToString() + " | " + Right.ToString() + ")";
    }
}

class DataNode<T> : Node
{
    T _data;
    public DataNode(T data)
    {
        _data = data;
    }
    public override string ToString()
    {
        return _data.ToString();
    }
}

Answer 7

How about something this simple:

class OrNode {
  string element;
  AndNode[] children;
} 

class AndNode {
  string element;
  OrNode[] children;
} 

Each class could have its own evaluate() which would AND or OR all the children as needed

You may still want to have a parent superclass so that your code could hold generic nodes without worrying about whether the first one was AND or OR.