Most efficient way to select point with the most surrounding points

Question

N.B: there's a major edit at the bottom of the question - check it out

Question

Say I have a set of points:

I want to find the point with the most points surrounding it, within radius 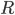(ie a circle) or within 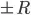(ie a square) of the point for 2 dimensions. I'll refer to it as the densest point function.

For the diagrams in this question, I'll represent the surrounding region as circles. In the image above, the middle point's surrounding region is shown in green. This middle point has the most surrounding points of all the points within radius 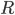and would be returned by the densest point function.

What I've tried

A viable way to solve this problem would be to use a range searching solution; this answer explains further and that it has "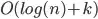 worst-case time". Using this, I could get the number of points surrounding each point and choose the point with largest surrounding point count.

However, if the points were extremely densely packed (in the order of a million), as such:

then each of these million points (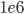) would need to have a range search performed. The worst-case time 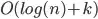, where is the number of points returned in the range, is true for the following point tree types:

• kd-trees of two dimensions (which are actually slightly worse, at ),
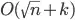• 2d-range trees,
• Quadtrees, which have a worst-case time of

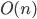
So, for a group of 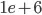points within radius 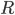of all points within the group, it gives complexity of 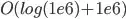for each point. This yields over a trillion operations!

Any ideas on a more efficient, precise way of achieving this, so that I could find the point with the most surrounding points for a group of points, and in a reasonable time (preferably 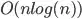or less)?

EDIT

Turns out that the method above is correct! I just need help implementing it.

(Semi-)Solution

If I use a 2d-range tree:

• A range reporting query costs 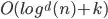, for 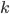returned points,
• For a range tree with fractional cascading (also known as layered range trees) the complexity is ,
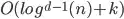• For 2 dimensions, that is ,
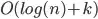• Furthermore, if I perform a range counting query (i.e., I do not report each point), then it costs .

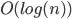I'd perform this on every point - yielding the 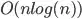complexity I desired!

Problem

However, I cannot figure out how to write the code for a counting query for a 2d layered range tree.

I've found a great resource (from page 113 onwards) about range trees, including 2d-range tree psuedocode. But I can't figure out how to introduce fractional cascading, nor how to correctly implement the counting query so that it is of O(log n) complexity.

I've also found two range tree implementations here and here in Java, and one in C++ here, although I'm not sure this uses fractional cascading as it states above the countInRange method that

It returns the number of such points in worst case * O(log(n)^d) time. It can also return the points that are in the rectangle in worst case * O(log(n)^d + k) time where k is the number of points that lie in the rectangle.

which suggests to me it does not apply fractional cascading.

Refined question

To answer the question above therefore, all I need to know is if there are any libraries with 2d-range trees with fractional cascading that have a range counting query of complexity 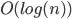so I don't go reinventing any wheels, or can you help me to write/modify the resources above to perform a query of that complexity?

Also not complaining if you can provide me with any other methods to achieve a range counting query of 2d points in 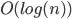in any other way!

Answer 1

I suggest using plane sweep algorithm. This allows one-dimensional range queries instead of 2-d queries. (Which is more efficient, simpler, and in case of square neighborhood does not require fractional cascading):

1. Sort points by Y-coordinate to array S.
2. Advance 3 pointers to array S: one (C) for currently inspected (center) point; other one, A (a little bit ahead) for nearest point at distance > R below C; and the last one, B (a little bit behind) for farthest point at distance < R above it.
3. Insert points pointed by A to Order statistic tree (ordered by coordinate X) and remove points pointed by B from this tree. Use this tree to find points at distance R to the left/right from C and use difference of these points' positions in the tree to get number of points in square area around C.
4. Use results of previous step to select "most surrounded" point.

This algorithm could be optimized if you rotate points (or just exchange X-Y coordinates) so that width of the occupied area is not larger than its height. Also you could cut points into vertical slices (with R-sized overlap) and process slices separately - if there are too many elements in the tree so that it does not fit in CPU cache (which is unlikely for only 1 million points). This algorithm (optimized or not) has time complexity O(n log n).

For circular neighborhood (if R is not too large and points are evenly distributed) you could approximate circle with several rectangles:

In this case step 2 of the algorithm should use more pointers to allow insertion/removal to/from several trees. And on step 3 you should do a linear search near points at proper distance (<=R) to distinguish points inside the circle from the points outside it.

Other way to deal with circular neighborhood is to approximate circle with rectangles of equal height (but here circle should be split into more pieces). This results in much simpler algorithm (where sorted arrays are used instead of order statistic trees):

1. Cut area occupied by points into horizontal slices, sort slices by Y, then sort points inside slices by X.
2. For each point in each slice, assume it to be a "center" point and do step 3.
3. For each nearby slice use binary search to find points with Euclidean distance close to R, then use linear search to tell "inside" points from "outside" ones. Stop linear search where the slice is completely inside the circle, and count remaining points by difference of positions in the array.
4. Use results of previous step to select "most surrounded" point.

This algorithm allows optimizations mentioned earlier as well as fractional cascading.

Answer 2

I would start by creating something like a https://en.wikipedia.org/wiki/K-d_tree, where you have a tree with points at the leaves and each node information about its descendants. At each node I would keep a count of the number of descendants, and a bounding box enclosing those descendants.

Now for each point I would recursively search the tree. At each node I visit, either all of the bounding box is within R of the current point, all of the bounding box is more than R away from the current point, or some of it is inside R and some outside R. In the first case I can use the count of the number of descendants of the current node to increase the count of points within R of the current point and return up one level of the recursion. In the second case I can simply return up one level of the recursion without incrementing anything. It is only in the intermediate case that I need to continue recursing down the tree.

So I can work out for each point the number of neighbours within R without checking every other point, and pick the point with the highest count.

If the points are spread out evenly then I think you will end up constructing a k-d tree where the lower levels are close to a regular grid, and I think if the grid is of size A x A then in the worst case R is large enough so that its boundary is a circle that intersects O(A) low level cells, so I think that if you have O(n) points you could expect this to cost about O(n * sqrt(n)).

Answer 3

You can speed up whatever algorithm you use by preprocessing your data in O(n) time to estimate the number of neighbouring points.

For a circle of radius R, create a grid whose cells have dimension R in both the x- and y-directions. For each point, determine to which cell it belongs. For a given cell c this test is easy:

c.x<=p.x && p.x<=c.x+R && c.y<=p.y && p.y<=c.y+R

(You may want to think deeply about whether a closed or half-open interval is correct.)

If you have relatively dense/homogeneous coverage, then you can use an array to store the values. If coverage is sparse/heterogeneous, you may wish to use a hashmap.

Now, consider a point on the grid. The extremal locations of a point within a cell are as indicated:

Points at the corners of the cell can only be neighbours with points in four cells. Points along an edge can be neighbours with points in six cells. Points not on an edge are neighbours with points in 7-9 cells. Since it's rare for a point to fall exactly on a corner or edge, we assume that any point in the focal cell is neighbours with the points in all 8 surrounding cells.

So, if a point p is in a cell (x,y), N[p] identifies the number of neighbours of p within radius R, and Np[y][x] denotes the number of points in cell (x,y), then N[p] is given by:

N[p] = Np[y][x]+
       Np[y][x-1]+
       Np[y-1][x-1]+
       Np[y-1][x]+
       Np[y-1][x+1]+
       Np[y][x+1]+
       Np[y+1][x+1]+
       Np[y+1][x]+
       Np[y+1][x-1]

Once we have the number of neighbours estimated for each point, we can heapify that data structure into a maxheap in O(n) time (with, e.g. make_heap). The structure is now a priority-queue and we can pull points off in O(log n) time per query ordered by their estimated number of neighbours.

Do this for the first point and use a O(log n + k) circle search (or some more clever algorithm) to determine the actual number of neighbours the point has. Make a note of this point in a variable best_found and update its N[p] value.

Peek at the top of the heap. If the estimated number of neighbours is less than N[best_found] then we are done. Otherwise, repeat the above operation.

To improve estimates you could use a finer grid, like so:

along with some clever sliding window techniques to reduce the amount of processing required (see, for instance, this answer for rectangular cases - for circular windows you should probably use a collection of FIFO queues). To increase security you can randomize the origin of the grid.

Considering again the example you posed:

It's clear that this heuristic has the potential to save considerable time: with the above grid, only a single expensive check would need to be performed in order to prove that the middle point has the most neighbours. Again, a higher-resolution grid will improve the estimates and decrease the number of expensive checks which need to be made.

You could, and should, use a similar bounding technique in conjunction with mcdowella's answers; however, his answer does not provide a good place to start looking, so it is possible to spend a lot of time exploring low-value points.