You can use a numerical solver to find the contour as follows:
% plot the distribution
figure;
x = (-5:0.5:5)';
y = (-5:0.5:5)';
[X1,X2] = meshgrid(x',y');
X = [X1(:) X2(:)];
p = mvncdf(X,mu,Sigma);
X3 = reshape(p,length(x),length(y));
surf(X1,X2,X3);
x = (-5:0.1:5)'; % define the x samples at which the contour should be calculated
y0 = zeros(size(x)); % initial guess
y = fsolve(@(y) mvncdf([x y], mu, Sigma) - 0.95, y0); % solve your problem
z = mvncdf([x y],mu,Sigma); % calculate the correspond cdf values
hold on
plot3(x(z>0.94), y(z>0.94), z(z>0.94), 'LineWidth', 5); % plot only the valid solutions, i.e. a solution does not exist for all sample points of x.
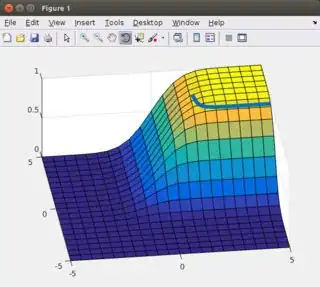
To obtain a better numerical representation of the desired contour, you can repeat the above approach for chosen y values. So, your line will better fill the whole graph.
As an alternative, one may use contour to calculate the points on the contour as follows:
figure
[c, h] = contour(X1, X2, X3, [0.95 0.95]);
c(3, :) = mvncdf(c',mu,Sigma);
figure(1)
plot3(c(1, :)', c(2, :)', c(3, :)', 'LineWidth', 5);
xlim([-5 5])
ylim([-5 5])
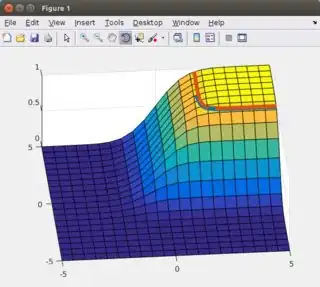
A disadvantage of this approach is that you do not have control over the coarseness of the sampled contour. Secondly, this method uses (interpolation of) the 3D cdf, which is less accurate than the values calculated with fsolve.