Given a directed graph, what is an algorithm I can use to find a random subset of its edges so that every node has exactly one incoming and exactly one outgoing edge?
For example, this could be the graph I am given:
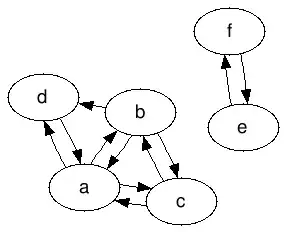
And this would be a valid output graph:
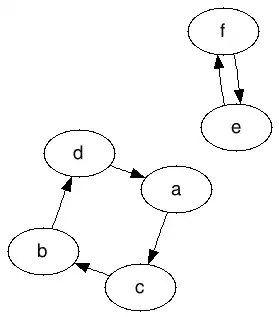
This is valid because:
- It contains all the nodes on the input graph
- All its edges are also on the input graph
- Every node has exactly one edge leaving it and one edge coming to it (and that can't be the same edge, no loops are allowed, every node has to connect to at least one other node).
If there is no possible solution that should be detected.
Is there an efficient algorithm to solve this?
Thanks!