Algorithm to rotate an array in linear time

Question

How to rotate an integer array by i times using swap function only in linear time.

Answer 1

You can do this in linear time by using a reverse() helper.

// rotate array of size=size, by n positions
void rotate(int array[], int size, int n)
{
  // reverse array[0...size-1]
  reverse(array, 0, size-1);

  // reverse A[0...n-1]
  reverse(array, 0, n-1);

  // reverse A[n...size-1]
  reverse(array, n, size-1);
}

// reverse elements in the array[pos_from ... pos_to]
void reverse(int array[], int pos_from, int pos_to)
{
   ...
}

Implementing reverse(int array[], int pos_from, int pos_to) using swaps is left as an exercise for the reader. Hint: This can be done in linear time.

Answer 2

Let us say we have a function called arr_reverse(arr,i,j) which reverses the elements of the array arr between index i and j using the swap function.

Example:

arr = {1,2,3,4,5} 
i = 0
j = 2

then the function will return:

{3,2,1,4,5} 
 ^^^^^

Implementing this function is straight forward and is O(N).

Now let's use this function in rotating the array.

arr     = {1,2,3,4,5} // input array
k       = 2 // amount of right rotation
result  = {4,5,1,2,3} // expected result 
l       = 5 // length of array.

Step 1: Call arr_reverse(arr,l-k,l-1) which is arr_reverse(arr,3,4)
we get {1,2,3,5,4} 
              ^^^

Step 2: Call arr_reverse(arr,0,l-k-1) which is arr_reverse(arr,0,2)
we get {3,2,1,5,4}
        ^^^^^     

Step 3: Call arr_reverse(arr,0,l-1) which is arr_reverse(arr,0,4)
we get {4,5,1,2,3} 
        ^^^^^^^^^

The entire process makes use of arr_reverse 3 times, making it O(N)

Answer 3

Here's a better solution, of a different nature than the others. It involves fewer array swaps than the others. Python:

import fractions
# rotates an array in-place i positions to the left, in linear time
def rotate(arr,i):
    n = len(arr)
    reps = fractions.gcd(n,i)
    swaps = n / reps
    for start in xrange(reps):
        ix = start
        tmp = arr[ix]
        for s in xrange(swaps-1):
            previx = ix
            ix = (ix + i) % n
            arr[previx] = arr[ix]
        arr[ix] = tmp
    return arr

Answer 4

Short Answer (python code)

def reverse(arr, i, j):
    for idx in xrange((j - i + 1) / 2):
        arr[i+idx], arr[j-idx] = arr[j-idx], arr[i+idx]

def solution(A, K):
    l = len(A)
    if l == 0:
        return []
    K = K%l
    reverse(A, l - K, l -1)
    reverse(A, 0, l - K -1)
    reverse(A, 0, l - 1)
    return A

Long Answer (code explanation)

Let me talk first the base case with K < N, the idea in this case is to split the array in two parts A and B, A is the first N-K elements array and B the last K elements. the algorithm reverse A and B separately and finally reverse the full array (with the two part reversed separately). To manage the case with K > N, think that every time you reverse the array N times you obtain the original array again so we can just use the module operator to find where to split the array (reversing only the really useful times avoiding useless shifting).

A graphical step by step example can help understanding better the concept. Note that

• The bold line indicate the the splitting point of the array (K = 3 in this example);
• The two red array indicate, respectively, the input and the expected output.

Starting from:

look that what we want in front of the final output will be the last 3 letter reversed, for now let reverse it in place (first reverse of the algorithm):

now reverse the first N-K elements (second reverse of the algorithm):

we already have the solution but in the opposite direction, we can solve it reversing the whole array (third and last reverse of the algorithm):

Here the final output, the original array cyclical rotated with K = 3.

Let give also another step by step example with python code, starting from:

A = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
K = 22
N = len(A)

we find the splitting index:

K = K%N
#2

because, in this case, the first 20 shift will be useless, now we reverse the last K (2) elements of the original array:

reverse(A, N-K, N-1)
# [1, 2, 3, 4, 5, 6, 7, 8, 10, 9]

as you can see 9 and 10 has been shift, now we reverse the first N-K elements:

reverse(A, 0, N-K-1)
# [8, 7, 6, 5, 4, 3, 2, 1, 10, 9]

And, finally, we reverse the full array:

reverse(A, 0, N-1)
# [9, 10, 1, 2, 3, 4, 5, 6, 7, 8]

Note that reversing an array have time complexity O(N).

Answer 5

Using linear time O(2N+m), and constant space O(4). m = GCD(n, p)

It's up to 50% faster than the swapping approach, because swapping requires writing O(N) times to a temporary.

http://www.eis.mdx.ac.uk/staffpages/r_bornat/oldteaching/I2A/slides%209%20circshift.pdf

for (m=0, count=0; count!=n; m++) {
    type t=A[m];
    for (i=m, j=m+p; j!=m; i=j, j = j+p<n ? j+p : j+p-n, count++)
        A[i]=A[j];
    A[i]=t; count++;
}

Answer 6

public int[] shift(int[] A, int K) {
    int N = A.length;
    if (N == 0)
        return A;
    int mid =  -K % N;
    if (mid < 0)
        mid += N;
    if (mid == 0)
        return A;

    reverseSubArray(A, 0 , mid - 1);

    reverseSubArray(A, mid , N - 1);

    reverseSubArray(A, 0 , N - 1);

    return A;
}

private void reverseSubArray(int[] A, int start , int end){
    int i = 0;
    int tmp;
    while (i < (end - start + 1) / 2) {
        tmp = A[i + start];
        A[i + start] = A[end - i];
        A[end - i] = tmp;
        i++;
    }

}

Doug McIlroy’s Handwaving Description

Answer 7

a naive pseudocode implementation:

for (n = 0; n < i; n++) {
    for (j = array.length-1; j > n; j--)
        swap(j, j-1)
}

Repeatedly moves the last element to the front, stopping before it moves anything previously moved to the front

Answer 8

This algorithm does (at most) len(array)-1 swaps, and works with both positive (right) and negative (left) rotation amounts. The array is modified in-place.
It doesn't require calculating the GCD, unlike other similar methods.

(Python 3)

def rotate(array,amount):
    if amount<0:
        amount+=len(array)
    a=0
    b=0
    for _ in range(len(array)-1):
        b=(b+amount) % len(array)
        if b==a:
            a+=1
            b=a
        if b!=a:
            array[a],array[b] = array[b],array[a] #swap array[a],array[b]
    return array

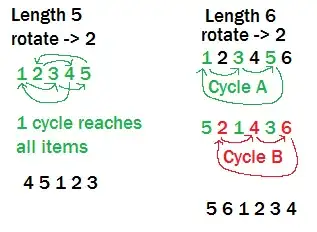
When one cycle is not enough (if it returns to the start before reaching every index), start a new cycle, from the next index.

Note: rotating items a, b, c, d, ... can be done using
swap a,b swap a,c swap a,d ...

Answer 9

Better use a direct and simple function, complexity N:

int rotate(int* a,int DIM,int rn,int* b) {
    int i; //counter 
    for(i=0;i<DIM;i++){ // looping through the array
        b[(i+rn)%len]=a[i]; // copying the values in the b array=a shifted with rn(+ for right or - for left shifting
}

Answer 10

/*
 * To change this template, choose Tools | Templates
 * and open the template in the editor.
 */
package rotateinlineartime;

/**
 *
 * @author Sunshine
 */
public class Rotator {

    void reverse(int a[], int n) {
        for (int i = 0; i <= n - 1; i++) {
            int temp;
            temp = a[i];
            a[i] = a[n - 1];
            a[n - 1] = temp;
            n--;
        }

        printArray(a);
    }

    void printArray(int a[]) {
        for (int i = 0; i < a.length; i++) {
            System.out.println(a[i]);
        }
    }
}

Answer 11

/* Q: How can we shift/rotate an array in place?
A: "in place" means O(1) space complexity, so we need to do some trick
 */

#include <iostream>
#include <algorithm>
using namespace std;

void ArrayRotate(int a[], int n, int k)
{
    if (n < 1 || k % n == 0 ) return;

    k %= n;
    if (k < 0) k += n;

    reverse(a, a+k);
    reverse(a+k, a+n);
    reverse(a, a+n);
}

void PrintArray(int a[], int n)
{
    for ( int i = 0 ; i < n; ++i)
        cout << a[i] << " ";
    cout << endl;
}

int main()
{
    int a[] = { 1, 2 , 3, 4, 5 };
    int n = sizeof(a)/sizeof (a[0]);

    PrintArray(a, n);
    ArrayRotate(a, n, 2);
    PrintArray(a, n);

    return 0;
}
/* Output:
1 2 3 4 5
3 4 5 1 2
 */

Answer 12

using only swap, following is a C++ implementation

template<class T>
void rotate_array(std::vector<T> *array, int i) {
  int n = array->size();
  i = i % n;
  int gcd_n_i = gcd(i, n);
  for (int j = 0; j < gcd_n_i; j++) {
    T first_element = array->at(j);
    for (int k = j; (k + i) % n != j; k = (k + i) % n) {
      std::swap(array->at(k), array->at((k + i) % n));
    }
  }
}

You can read more about it at http://pointer-overloading.blogspot.in/2013/09/algorithms-rotating-one-dimensional.html

Answer 13

void reverse_array(int a[], int start, int end){

    while(start < end){     
            int temp =  a[start];
            a[start] = a[end];
            a[end] = temp;
            start++;
            end--;
    }

}

void rotate_array(int a[], int pivot, int len){
    int i;
    /*Reverse the whole array */
    reverse_array(a, 0, len);

    /* Reverse from 0 to pivot and pivot to end */
    reverse_array(a,0, pivot);
    reverse_array(a,pivot+1,len);

}

Answer 14

Here's a small snippet thats works in O(n), written in JavaScript. The keyconcept is, that you always have to work with the replaced item.

function swap(arr, a, v) {
    var old = arr[a];
    arr[a] = v;
    return old;
}

function rotate(arr, n) {
    var length = arr.length;
    n = n % length;
    if(!n) return arr;

    for(var cnt = 0, 
            index = 0,
            value = arr[index],
            startIndex = index; 
        cnt < length; 
        cnt++) {

        // Calc next index
        var nextIndex = mapIndex(index, n, length);

        // Swap value with next
        value = swap(arr, nextIndex, value)

        if(nextIndex == startIndex) {
            startIndex = index = mapIndex(index, 1, length);
            value = arr[index];
        } else {
            index = nextIndex;
        }
    }

    return arr;
}

function mapIndex(index, n, length) {
    return (index - n + length) % length;
}

console.log(rotate([1,2,3,4,5,6,7,8,9], 5))
console.log(rotate([1,2,3,4,5,6], 2))

Answer 15

An O(1) method of accomplishing this, in python:

class OffsetList(list):
    __slots__ = 'offset'
    def __init__(self, init=[], offset=-1):
        super(OffsetList, self).__init__(init)
        self.offset = offset
    def __getitem__(self, key):
        return super(OffsetList, self).__getitem__(key + self.offset)
    def __setitem__(self, key, value):
        return super(OffsetList, self).__setitem__(key + self.offset, value)
    def __delitem__(self, key):
        return super(OffsetList, self).__delitem__(key + self.offset)
    def index(self, *args):
        return super(OffsetList, self).index(*args) - self.offset

This is based on this answer about using a 1-based list in python.

This does have the slight glitch that if you attempt to index an item off the end of the list, it will return items from the (new) beginning, and negative indicies less than the size minus the offset won't work.

Answer 16

here is my answer using js hope this helps where k is the number of the rotations you want to preform

 var arrayRoatate=function(array,k){
    for(;k>0;k--) {
     var nextElementValue=undefined;
        for (var i = 0; i < array.length; i=i+2) {
            var nextElement = i + 1;
            if (nextElement >= array.length)
                nextElement = nextElement - array.length;
            var tmp=array[i];
            if(nextElementValue!==undefined)
                array[i]=nextElementValue
            nextElementValue=array[nextElement];
            array[nextElement]=tmp;

        }
    }
return array;

Answer 17

For circular right rotation.

public static void main(String[] args) {
    Scanner scan = new Scanner(System.in);
    int n = scan.nextInt();
    int k = scan.nextInt() % n;
    int q = scan.nextInt();
    int arr[] = new int[n];

    for (int i = 0; i < n; i++) 
    {
        int a = i + k;
        int pos = (a < n) ? a : a - n;
        arr[pos] = scan.nextInt();
    }
    for (int j = 0; j < q; j++) 
    {
        System.out.println(arr[scan.nextInt()]);
    }
}

Answer 18

why only swap function?

O(n) in time and space:

var rotateCount = 1;
var arr = new Array(1,2,3,4,5,6,7,8,9,10);

tmp = new Array(arr.length);
for (var i = 0; i<arr.length; i++)
    tmp[(i+rotateCount)%arr.length]=arr[i];
arr = tmp;

alert(arr);

Answer 19

My solution with java

static int[] rotLeft(int[] a, int d) {
    for (int i = 0; i < d; i++) {
        oneRotation(a);
    }
    return a;
}

static void oneRotation(int[] a) {
    int firstElement = a[0];
    for (int i = 0; i < a.length - 1; i++) {
        a[i] = a[i + 1];
    }
    a[a.length - 1] = firstElement;
}

Answer 20

public static String rotateKTimes(String str,int k){
    int n = str.length();

    //java substring has O(n) complexity
    return str.substring(n-k) + str.substring(0,n-k);
}

Answer 21

Simple Solution in O(n) time and using O(1) space:
for e.g 1,2,3,4,5,6,7
rotating 2 times 
start with index 2, store a[0] as last
Iteration 1: 1,2,1,4,3,6,5 (1-->3-->5-->7)
Iteration 2: 1,7,1,2,3,4,5 (2-->4-->6)
replace 1 with 6 (last value).

public int[] roatateArray(int[] a,int k)
{
    int last = a[0];
    int start = k;
    for(int j=0;j<k;j++) {
    for(int i=start;i<a.length;i+=k)
    {
        int tmp=a[i];
        a[i]=last;
        last=tmp;
    }
    start--;
    if (start<=0) break;
    }
    a[0]=last;
    return a;
}

Answer 22

void rotate(int array [], int n, int k)
{
    int temp1,temp2;     //two variable to hold values
    int visited,count,index;   //'visited' to check if cycle 
                               // collides with index
                               //'count' to check number of loops
    visited = n-1;
    temp1 = array[n-1];
    index = n-1;
    count = 0;

    while(count<n)
    {   
        temp2 = temp1;
        temp1 = array[(n+index-k)%n];
        array[(n+index-k)%n] = temp2;
        index = (n+index-k)%n;
        if (index == visited)
        {   
            cout<<"\nindex == visited at index = "<<index;
            getch();
            index--;
            visited=index;
            temp1=array[index];
        }
        count++;
        cout<<"\ncount is : "<<count;
        cout<<"\narray is : ";
        p_all_arr(array,0,n); //display arr 
        getch();
    }

}