Plot equally spaced markers along a spiral

Question

I want to move a red star marker along the spiral trajectory with an equal distance of 5 units between the red star points on its circumference like in the below image.

vertspacing = 10;
horzspacing = 10;
thetamax = 10*pi;
% Calculation of (x,y) - underlying archimedean spiral.
b = vertspacing/2/pi;
theta = 0:0.01:thetamax;
x = b*theta.*cos(theta)+50;
y = b*theta.*sin(theta)+50;

% Calculation of equidistant (xi,yi) points on spiral.
smax = 0.5*b*thetamax.*thetamax;
s = 0:horzspacing:smax;
thetai = sqrt(2*s/b);
xi = b*thetai.*cos(thetai);
yi = b*thetai.*sin(thetai);
plot(x,y,'b-');
hold on

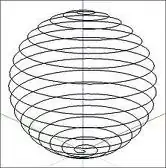
I want to get a figure that looks like the following:

This is my code for the circle trajectory:

% Initialization steps.
format long g;
format compact;
fontSize = 20;
r1 = 50;
r2 = 35;
r3=  20;
xc = 50;
yc = 50;
% Since arclength = radius * (angle in radians),
% (angle in radians) = arclength / radius = 5 / radius.
deltaAngle1 = 5 / r1;
deltaAngle2 = 5 / r2;
deltaAngle3 = 5 / r3;
theta1 = 0 : deltaAngle1 : (2 * pi);
theta2 = 0 : deltaAngle2 : (2 * pi);
theta3 = 0 : deltaAngle3 : (2 * pi);
x1 = r1*cos(theta1) + xc;
y1 = r1*sin(theta1) + yc;
x2 = r2*cos(theta2) + xc;
y2 = r2*sin(theta2) + yc;
x3 = r3*cos(theta3) + xc;
y3 = r3*sin(theta3) + yc;
plot(x1,y1,'color',[1 0.5 0])
hold on
plot(x2,y2,'color',[1 0.5 0])
hold on
plot(x3,y3,'color',[1 0.5 0])
hold on

% Connecting Line:
plot([70 100], [50 50],'color',[1 0.5 0])
% Set up figure properties:
% Enlarge figure to full screen.
set(gcf, 'Units', 'Normalized', 'OuterPosition', [0, 0, 1, 1]);
drawnow;
axis square;
for i = 1 : length(theta1)
    plot(x1(i),y1(i),'r*')
    pause(0.1)
end
for i = 1 : length(theta2)
    plot(x2(i),y2(i),'r*')
    pause(0.1)
end
for i = 1 : length(theta3)
    plot(x3(i),y3(i),'r*')    
    pause(0.1)
end

Answer 1

I can't think of a way to compute distance along a spiral, so I'm approximating it with circles, in hopes that it will still be useful.

My solution relies on the InterX function from FEX, to find the intersection of circles with the spiral. I am providing an animation so it is easier to understand.

The code (tested on R2017a):

function [x,y,xi,yi] = q44916610(doPlot)
%% Input handling:
if nargin < 1 || isempty(doPlot)
  doPlot = false;
end
%% Initialization:
origin = [50,50];
vertspacing = 10;
thetamax = 5*(2*pi);
%% Calculation of (x,y) - underlying archimedean spiral.
b = vertspacing/(2*pi);
theta = 0:0.01:thetamax;
x = b*theta.*cos(theta) + origin(1);
y = b*theta.*sin(theta) + origin(2);
%% Calculation of equidistant (xi,yi) points on spiral.
DST = 5; cRes = 360; 
numPts = ceil(vertspacing*thetamax); % Preallocation
[xi,yi] = deal(NaN(numPts,1));

if doPlot && isHG2() % Plots are only enabled if the MATLAB version is new enough.
  figure(); plot(x,y,'b-'); hold on; axis equal; grid on; grid minor;
  hAx = gca; hAx.XLim = [-5 105]; hAx.YLim = [-5 105];
  hP = plot(xi,yi,'r*');
else
  hP = struct('XData',xi,'YData',yi);
end
hP.XData(1) = origin(1); hP.YData(1) = origin(2);
for ind = 2:numPts
  P = InterX([x;y], makeCircle([hP.XData(ind-1),hP.YData(ind-1)],DST/2,cRes));  
  [~,I] = max(abs(P(1,:)-origin(1)+1i*(P(2,:)-origin(2))));
  if doPlot, pause(0.1); end
  hP.XData(ind) = P(1,I); hP.YData(ind) = P(2,I);
  if doPlot, pause(0.1); delete(hAx.Children(1)); end
end
xi = hP.XData(~isnan(hP.XData)); yi = hP.YData(~isnan(hP.YData));

%% Nested function(s):
function [XY] = makeCircle(cnt, R, nPts)
  P = (cnt(1)+1i*cnt(2))+R*exp(linspace(0,1,nPts)*pi*2i);
  if doPlot, plot(P,'Color',lines(1)); end
  XY = [real(P); imag(P)];
end

end

%% Local function(s):
function tf = isHG2()
  try
    tf = ~verLessThan('MATLAB', '8.4');
  catch
    tf = false;
  end
end

function P = InterX(L1,varargin)
    % DOCUMENTATION REMOVED. For a full version go to:
    % https://www.mathworks.com/matlabcentral/fileexchange/22441-curve-intersections

    narginchk(1,2);
    if nargin == 1
        L2 = L1;    hF = @lt;   %...Avoid the inclusion of common points
    else
        L2 = varargin{1}; hF = @le;
    end

    %...Preliminary stuff
    x1  = L1(1,:)';  x2 = L2(1,:);
    y1  = L1(2,:)';  y2 = L2(2,:);
    dx1 = diff(x1); dy1 = diff(y1);
    dx2 = diff(x2); dy2 = diff(y2);

    %...Determine 'signed distances'   
    S1 = dx1.*y1(1:end-1) - dy1.*x1(1:end-1);
    S2 = dx2.*y2(1:end-1) - dy2.*x2(1:end-1);

    C1 = feval(hF,D(bsxfun(@times,dx1,y2)-bsxfun(@times,dy1,x2),S1),0);
    C2 = feval(hF,D((bsxfun(@times,y1,dx2)-bsxfun(@times,x1,dy2))',S2'),0)';

    %...Obtain the segments where an intersection is expected
    [i,j] = find(C1 & C2); 
    if isempty(i), P = zeros(2,0); return; end

    %...Transpose and prepare for output
    i=i'; dx2=dx2'; dy2=dy2'; S2 = S2';
    L = dy2(j).*dx1(i) - dy1(i).*dx2(j);
    i = i(L~=0); j=j(L~=0); L=L(L~=0);  %...Avoid divisions by 0

    %...Solve system of eqs to get the common points
    P = unique([dx2(j).*S1(i) - dx1(i).*S2(j), ...
                dy2(j).*S1(i) - dy1(i).*S2(j)]./[L L],'rows')';

    function u = D(x,y)
        u = bsxfun(@minus,x(:,1:end-1),y).*bsxfun(@minus,x(:,2:end),y);
    end
end

Result:

Note that in the animation above, the diameter of the circle (and hence the distance between the red points) is 10 and not 5.