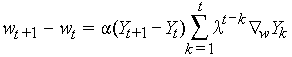openCV: How to use getPerspectiveTransform

Question

I have an image represented by a matrix of size n * n

I've created a transform matrix

M = cv2.getPerspectiveTransform(...)

And I can transform the image with the shape defined in M using

cv2.warpPerspective(image, M, image_shape)

According to this, I should be able to multiply the matrix with a point and get the new location of that point, after the transformation. I tried that:

point = [100, 100, 0]
x, y, z = M.dot(point)

But I got the wrong results. (In this case [112.5 12.5 0])

What am I doing wrong?

For more clarity, here's what I'm doing:

I have this image, with the lines and the square on different layers

I warp the lines and get this:

And now I want to get the coordinates for putting the square like this:

What I have is the warp matrix I used for the lines, and the coordinates of the square in the first picture

Note: one option is to create an image with a single dot, just warp it with the first method and find the non-zero cells in the new image. I'm looking for something more idiomatic than that, hopefully

Possible duplicate of [Opencv homography to find global xy coordinates from pixel xy coordinates](https://stackoverflow.com/questions/44578876/opencv-homography-to-find-global-xy-coordinates-from-pixel-xy-coordinates) — alkasm, Jul 10 '17 at 11:34
If you see the link you are giving, it says the last element of `point` should be 1, and you use 0!!... — api55, Jul 10 '17 at 11:47

alkasm · Accepted Answer · 2017-07-10T12:45:33.490

The last point of a homogeneous coordinate should never be 0 unless it is specifically referencing a point at infinity. For your purposes, it should be 1. You should also scale the transformed pixels x and y by the last value z. See my answer here for an in-depth explanation.

For a single point:

point = np.array([100, 100])
homg_point = [point[0], point[1], 1] # homogeneous coords
transf_homg_point = M.dot(homg_point) # transform
transf_homg_point /= transf_homg_point[2] # scale
transf_point = transf_homg_point[:2] # remove Cartesian coords

For multiple points (with the standard way that OpenCV writes points):

points = np.array([[[100, 100]], [[150,100]], [[150,150]], [[150,100]]])
homg_points = np.array([[x, y, 1] for [[x, y]] in points]).T
transf_homg_points = M.dot(homg_points)
transf_homg_points /= transf_homg_points[2]
transf_points = np.array([[[x,y]] for [x, y] in transf_homg_points[:2].T])

A minimal example using points grabbed from an OpenCV function:

import numpy as np 
import cv2

# generate random noise image, draw a white box
img = np.random.rand(512,512,3)
img[128:384, 64:196] = [1,1,1]

# create a Euclidean transformation which rotates by 30 deg + translates by (100,100)
theta = 30*np.pi/180
H = np.array([
    [ np.cos(theta),np.sin(theta),100.],
    [-np.sin(theta),np.cos(theta),100.],
    [0.,0.,1.]])

# find the white box
bin_img = cv2.inRange(img, np.ones(3), np.ones(3))
contour_points = cv2.findContours(bin_img, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)[1][0]

# transform the location of the box
homg_points = np.array([[x, y, 1] for [[x, y]] in contour_points]).T
transf_homg_points = H.dot(homg_points)
transf_homg_points /= transf_homg_points[2]
transf_rect = np.array([[[x,y]] for [x, y] in transf_homg_points[:2].T], dtype=np.int32)

# draw the transformed box as a green outline
cv2.polylines(img, [transf_rect], isClosed=True, color=[0,1,0], thickness=2)

Yielding an image with random noise, a white box, and a green outline which shows the transformation applied to the box contours.

openCV: How to use getPerspectiveTransform

1 Answers1