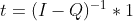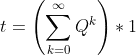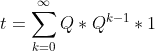Best iterative way to calculate the fundamental matrix of an absorbing Markov Chain?

Question

I have a very large absorbing Markov chain. I want to obtain the fundamental matrix of this chain to calculate the expected number of steps before absortion. From this question I know that this can be calculated by the equation

(I - Q)t=1

which can be obtained by using the following python code:

def expected_steps_fast(Q):
    I = numpy.identity(Q.shape[0])
    o = numpy.ones(Q.shape[0])
    numpy.linalg.solve(I-Q, o)

However, I would like to calculate it using some kind of iterative method similar to the power iteration method used for calculate the PageRank. This method would allow me to calculate an approximation to the expected number of steps before absortion in a mapreduce-like system.

¿Does something similar exist?

Have you looked at iterative solvers for systems of linear equations like GMRES? They provide some error estimates to check how many iterations you need. Python provides them in [`scipy.sparse.linalg`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.linalg.gmres.html#scipy.sparse.linalg.gmres) — Tobias Ribizel, Jul 18 '17 at 10:48
Ah sorry, I misunderstood your question! Have you looked at the [Neumann series representation](https://en.wikipedia.org/wiki/Absorbing_Markov_chain#Fundamental_matrix) of the fundamental matrix? It might be possible to approximate the inverse using only a limited number of summands from the power series — Tobias Ribizel, Jul 18 '17 at 10:52
Thanks for your comments @TobiasRibizel. I think that the Neumann series is not what I am searching because it would imply to multiply the matrix several times. However, if I understand correctly the GMRES algorithm, this solution might be parallelized in a per-component basis. — Carlos Perez-Miguel, Jul 18 '17 at 11:09

score 0 · Answer 1 · answered Jul 19 '17 at 11:47

If you have a sparse matrix, check if scipy.spare.linalg.spsolve works. No guarantees about numerical robustness, but at least for trivial examples it's significantly faster than solving with dense matrices.

import networkx as nx
import numpy as np
import scipy.sparse as sp
import scipy.sparse.linalg as spla

def example(n):
    """Generate a very simple transition matrix from a directed graph
    """
    g = nx.DiGraph()
    for i in xrange(n-1):
        g.add_edge(i+1, i)
        g.add_edge(i, i+1)
    g.add_edge(n-1, n)
    g.add_edge(n, n)
    m = nx.to_numpy_matrix(g)
    # normalize rows to ensure m is a valid right stochastic matrix
    m = m / np.sum(m, axis=1)
    return m

A = sp.csr_matrix(example(2000)[:-1,:-1])
Ad = np.array(A.todense())

def sp_solve(Q):
    I = sp.identity(Q.shape[0], format='csr')
    o = np.ones(Q.shape[0])
    return spla.spsolve(I-Q, o)

def dense_solve(Q):
    I = numpy.identity(Q.shape[0])
    o = numpy.ones(Q.shape[0])
    return numpy.linalg.solve(I-Q, o)

Timings for sparse solution:

%timeit sparse_solve(A)
1000 loops, best of 3: 1.08 ms per loop

Timings for dense solution:

%timeit dense_solve(Ad)
1 loops, best of 3: 216 ms per loop

Like Tobias mentions in the comments, I would have expected other solvers to outperform the generic one, and they may for very large systems. For this toy example, the generic solve seems to work well enough.

Thanks for your answer Andrew, however I am searching for a method that could be calculated in parallel for all the elements of the solution. Following the GMRES method proposed by Tobias I found other iterative methods like the [Jacobi method](https://en.wikipedia.org/wiki/Jacobi_method) that could fulfill my requirements. — Carlos Perez-Miguel, Jul 19 '17 at 13:38

score 0 · Answer 2 · answered Jul 31 '17 at 10:29

I arraived to this answer thanks to @tobias-ribizel's suggestion of using the Neumann series. If we part from the following equation:

t=(I-Q)^-1 1

Using the Neumann series:

t=sum_0_inf(Q^k)1

If we multiply each term of the series by the vector 1 we could operate separately over each row of the matrix Q and approximate successively with:

t=sum_0_inf(Q*Q^k-1*1)

This is the python code I use to calculate this:

def expected_steps_iterative(Q, n=10):
    N = Q.shape[0]
    acc = np.ones(N)
    r_k_1 = np.ones(N)
    for k in range(1, n):
        r_k = np.zeros(N)
        for i in range(N):
            for j in range(N):
                r_k[i] += r_k_1[j] * Q[i, j]
        if np.allclose(acc, acc+r_k, rtol=1e-8):
            acc += r_k
            break
        acc += r_k
        r_k_1 = r_k
    return acc

And this is the code using Spark. This code expects that Q is a RDD where each row is a tuple (row_id, dict of weights for that row of the matrix).

def expected_steps_spark(sc, Q, n=10):
    def dict2np(d, sz):
        vec = np.zeros(sz)
        for k, v in d.iteritems():
            vec[k] = v
        return vec
    sz = Q.count()
    acc = np.ones(sz)
    x = {i:1.0 for i in range(sz)}
    for k in range(1, n):
        bc_x = sc.broadcast(x)
        x_old = x
        x = Q.map(lambda (u, ol): (u, reduce(lambda s, j: s + bc_x.value[j]*ol[j], ol, 0.0)))
        x = x.collectAsMap()
        v_old = dict2np(x_old, sz)
        v = dict2np(x, sz)
        acc += v
        if np.allclose(v, v_old, rtol=1e-8):
            break
    return acc

Best iterative way to calculate the fundamental matrix of an absorbing Markov Chain?

2 Answers2