If you are moving horizontally, you can increment the longitude by distance / (R * cos(lat)). No atan needed.
EDIT: Since you wanted a formula for the general case, consider the following geometric derivation:
Front view:
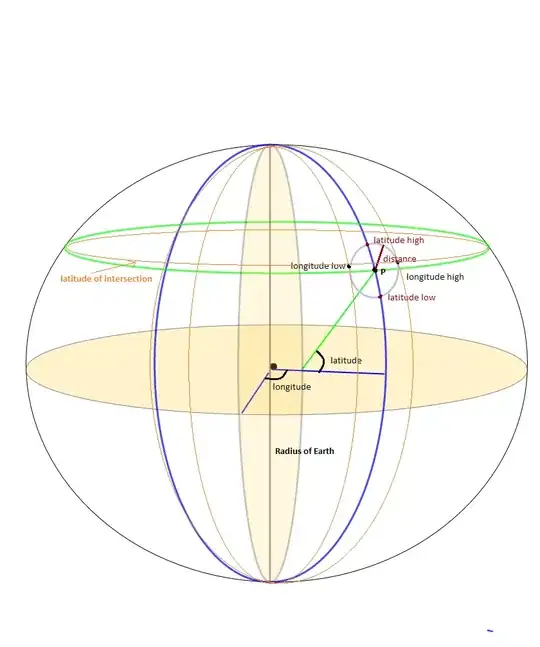
Side view:

Entire setup:
Notes:
r is the unit vector of your starting position, and s is the endpoint.
a, b, c are intermediate vectors to aid calculation.
(θ, φ) are the (lat, long) coordinates.γ is the bearing of the direction you are going to travel in.δ is the angle travelled through (distance / radius R = 6400000m).
We need a, b to be perpendicular to r and also a aligned with North. This gives:
c is given by (simple trigonometry):

And thus we get s (through some very tedious algebra):
Now we can calculate the final (lat, long) coordinates of s using:
Code:
function deg2rad(deg) { return deg * (Math.PI / 180.0) }
function rad2deg(rad) { return rad * (180.0 / Math.PI) }
function getFinalLatLong(lat1, long1, distance, angle, radius) {
// calculate angles
var delta = distance / radius,
theta = deg2rad(lat1),
phi = deg2rad(long1),
gamma = deg2rad(angle);
// calculate sines and cosines
var c_theta = Math.cos(theta), s_theta = Math.sin(theta);
var c_phi = Math.cos(phi) , s_phi = Math.sin(phi) ;
var c_delta = Math.cos(delta), s_delta = Math.sin(delta);
var c_gamma = Math.cos(gamma), s_gamma = Math.sin(gamma);
// calculate end vector
var x = c_delta * c_theta * c_phi - s_delta * (s_theta * c_phi * c_gamma + s_phi * s_gamma);
var y = c_delta * c_theta * s_phi - s_delta * (s_theta * s_phi * c_gamma - c_phi * s_gamma);
var z = s_delta * c_theta * c_gamma + c_delta * s_theta;
// calculate end lat long
var theta2 = Math.asin(z), phi2 = Math.atan2(y, x);
return [rad2deg(theta2), rad2deg(phi2)];
}
Test cases:
Input (lat, long) = (45, 0), angle = 0, distance = radius * deg2rad(90) => (45, 180) (as I said before)
Input (lat, long) = (0, 0), angle = 90, distance = radius * deg2rad(90) => (0, 90) (as expected - start at equator, travel east by 90 longitude)
Input (lat, long) = (54, 29), angle = 36, distance = radius * deg2rad(360) => (54, 29) (as expected - start at any random position and go full-circle in any direction)
Interesting case: input (lat, long) = (30, 0), everything else same. => (0, 90) (we expected (30, 90)? - not starting at equator, travel by 90 degrees to North)
The reason for this is that 90 degrees to North is not East (if you're not at the equator)! This diagram should show why:
As you can see, the path of movement at 90 degrees to the North is not in the direction of East.








