0

Here is the problem I am problem I am trying to solve. I have a set of "Like" elements that define a person liking another person. For example, one element would have the information "John likes Jane". Another might have "Jane likes Joseph" and so on. I would like to know what would be the best algorithm to determine

  1. Least number of elements that together would forma closed loop. In the above example, if we have another element "Joseph likes John" then the 3 elements together would form a closed loop
  2. The list of elements could be huge

I was looking at the Travelling Salesman algorithm. But it doesnt provide me the Least number of nodes to form a closed loop

Appreciate your help

user8396597
  • 1
  • Dykstra's anyone? Depends on how you store the relations, a MVCE would be nice. Graph seems like the option here as the matrix would be sparse. https://stackoverflow.com/help/how-to-ask The algorithm will differ greatly depending on your data structure – JimLohse Jul 31 '17 at 23:18
  • Also see this great answer to a [similarly vague question](https://stackoverflow.com/questions/26857842/find-shortest-path/) :) https://stackoverflow.com/a/26858645/3255525 – JimLohse Jul 31 '17 at 23:21
  • 1
    Possible duplicate of [Find cycle of shortest length in a directed graph with positive weights](https://stackoverflow.com/questions/3911626/find-cycle-of-shortest-length-in-a-directed-graph-with-positive-weights) – djhaskin987 Jul 31 '17 at 23:21
  • As I commented above, this is really a graph problem. The people are the nodes and the edges are people liking other people. Each edge in your problem has weight 1, and you want to find the smallest cycle (what most mathematicians call your "loop") in a given graph (set of "who likes who" data). – djhaskin987 Jul 31 '17 at 23:24
  • Dijkstra’s algorithm requires all the elements to be part of the final closed loop. in my case, out of say 100 elements, the above 3 elements simply form a closed loop. So I dont care about the other 97 – user8396597 Jul 31 '17 at 23:28

2 Answers2

0

Start with the first person.

Follow the chain of people they like, storing each each person inside an array. Once you reach a duplicate person it means you have reached a loop, To find the length of this loop you find the 2 occurences of the person say in personarr[X] and personarr[Y] and do Y - X. Store the length of this loop along with any member inside it.

Now, making sure to keep your personarr[] you will move onto the second person. If they are not in the array then add them to it and repeat first step, otherwise move onto third person. Each time you find a new loop update your 'best loop' information.

Theo Walton
  • 1,085
  • 9
  • 24
  • This method was my first instinct, but I think it assumes that each person has a unique like... for example you may have two elements "Bob likes Jim" and "Bob likes Sue"... so which one gets to join your chain? – arbuthnott Aug 01 '17 at 00:09
  • oh I assumed that each person likes only one person – Theo Walton Aug 01 '17 at 00:12
0

First you need to realize that in the worst case here you have to go over the entire list of elements at least once.

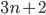An example which show this is a graph with 3n+2 vertices in which each triplet of the first 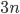3n vertices forms a triangle and the last 2 vertices "like" each other. You have to find those two in order to see that the least number of elements you're looking for is 2, and in the worst case you find them last, just like when you're looking for your keys.

After you realize this your question basically becomes the question of finding the smallest cycle in an unweighted directed graph. The best solution I can think of right now is running BFS from each node to find the shortest cycle to itself and then taking the minimum of all results. The run time complexity for this is O(V^2).

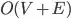I performed a quick search and found this post in which what I just said is suggested with someone claiming it's the best way to do it. There's also an answer suggesting another way by using DFS, which takes O(V+E), but since 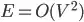E=O(V^2) it doesn't asymptotically improve anything in the worst case.

Tomer Godinger
  • 370
  • 3
  • 9