I came upon two resources and they appear to say the basic definition in two ways.
Source 1 (and one of my professor) says:
All leaves are at the same level and all non-leaf nodes have two child nodes.
Source 2 (and 95% of internet) says:
A full binary tree (sometimes referred to as a proper or plane binary tree) is a tree in which every node in the tree has either 0 or 2 children.
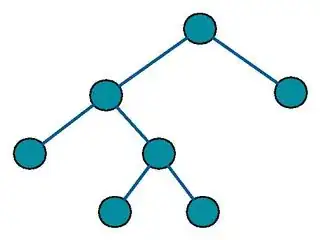
becomes a binary tree but not according to Source 1 as the leaves are not in the same level.
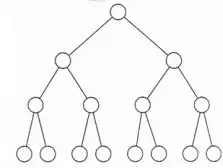
So typically they consider trees like,
as Full Binary Tree.
I may sound stupid but I'm confused what to believe. Any help is appreciated. Thanks in advance.