Detect Networks/communities and assign IDs

Question

i have a table which shows two columns having IDs. The below table implies that ID in column 1 is related to ID in column 2. The schema of table is such that we have both ( say IDs are A and B , both are related. Then entry will appear twice , once as A to B and B to A ) , sample table below :

ID.1    ID.2
 A       B 
 A       C
 B       C
 C       B
 C       A
 B       A
 D       E
 E       F
 F       E
 D       F
 E       D
 F       D

( e.g. for A,B,C we see A & B are related , A & C are related , B & C are related - i tag all of them in one house and give a unique id )

Output

  ID.1    ID.2      HouseID
     A       B       X1
     A       C       X1
     B       C       X1
     C       B       X1
     C       A       X1
     B       A       X1
     D       E       X2
     E       F       X2
     F       E       X2
     D       F       X2 
     D       F       X2
     E       D       X2
     F       D       X2

How do i get the above in R ? what if i add a transitive logic for example A is related to B and A is related to C , Hence B also must know C ?

A few keywords: in your 1st case, you're after (maximal) [cliques](https://en.wikipedia.org/wiki/Clique_(graph_theory)), whereas your 2nd case (with "transitive logic") is about [connected components](https://en.wikipedia.org/wiki/Connected_component_(graph_theory)). Both cases can be addressed using [igraph](https://cran.r-project.org/package=igraph). Note that your 2nd case is well-defined, since connected components realize a partition of the graph. Your 1st case is not: a vertex can belong to 2 different maximal cliques. — Scarabee, Aug 10 '17 at 11:19
Example for 2nd case: https://stackoverflow.com/questions/45079559/make-a-group-indices-based-on-several-columns — Scarabee, Aug 10 '17 at 11:20
@Scarabee - 2nd case inputs understood and easy to implement. From a definition standpoint i call the second case a community whereas first case i call a household - hence a person A can belong to multiple households and one community. This is what you imply by 'can belong to 2 different maximal cliques' ? How do i address this case — Learner_seeker, Aug 11 '17 at 00:48
How can it detect ( A related to B , B related to C , A related to C , A related to D ) are one house since a direct relation has been identified in all pairs from A and BC is captured in the same house id rather than a separate one - pairs ( AB , AC , AD , BC) — Learner_seeker, Aug 11 '17 at 00:51
I am using the same code as the link shared above , however i am getting NAs for the group values `g <- graph_from_data_frame(df1[, c(2, 3, 1)]) myGroups <- components(g)$membership df1$group <- myGroups[df1$G1]` — Learner_seeker, Aug 11 '17 at 01:59
Yes it is what I imply. A person can belong to multiple households but you want only one HouseID column, so you have to choose one. / Despite your example, the way you identify households is still not clear enough for me. / No I don't think you could do it using only dplyr. / Using the sample you provided, `g <- graph_from_data_frame(df1[, 1:2]);myGroups <- components(g)$membership;df1$group <- myGroups[df1$ID.1]` does work. — Scarabee, Aug 11 '17 at 13:14

score 2 · Accepted Answer · answered Aug 12 '17 at 06:59

2

As I understand the question, @Scarabee had it right. The answer depends on maximal cliques, but the bounty shows that the OP did not consider that a full answer. This answer pushes that through to assigning the HouseID.

library(igraph)

## Your sample data
Edges1 = read.table(text="ID.1    ID.2
 A       B 
 A       C
 B       C
 C       B
 C       A
 B       A
 D       E
 E       F
 F       E
 D       F
 E       D
 F       D", 
header=TRUE, stringsAsFactors=FALSE)

g1 = graph_from_edgelist(as.matrix(Edges1), directed=FALSE)
plot(g1)
MC1 = max_cliques(g1)
MC1
[[1]]
+ 3/6 vertices, named, from 8123133:
[1] A B C

[[2]]
+ 3/6 vertices, named, from 8123133:
[1] D E F

This gives the maximal cliques (the houses), but we need to construct the HouseID variable.

Edges1$HouseID = apply(Edges1, 1, 
    function(e) 
        which(sapply(MC1, function(mc) all(e %in% names(unclass(mc))))))
Edges1
   ID.1 ID.2 HouseID
1     A    B       1
2     A    C       1
3     B    C       1
4     C    B       1
5     C    A       1
6     B    A       1
7     D    E       2
8     E    F       2
9     F    E       2
10    D    F       2
11    E    D       2
12    F    D       2

The outer apply loops through the edges. The inner sapply checks which clique (house) contains both nodes from the edge.

This provides the structure that the question asked for. But as @Scarabee pointed out, a node may belong to more than one maximal clique (house). That is not exactly a problem as the requested structure assigns the HouseID to edges. Here is an example with a node that belongs to two houses.

Edges3 = read.table(text="ID.1    ID.2
 A       B 
 A       C
 B       C
 D       E
 D       A
 E       A", 
header=TRUE, stringsAsFactors=FALSE)

g3 = graph_from_edgelist(as.matrix(Edges3), directed=FALSE)
plot(g3)
MC3 = max_cliques(g3)

Edges3$HouseID = apply(Edges3, 1, 
    function(e) 
        which(sapply(MC3, function(mc) all(e %in% names(unclass(mc))))))
Edges3
  ID.1 ID.2 HouseID
1    A    B       2
2    A    C       2
3    B    C       2
4    D    E       1
5    D    A       1
6    E    A       1

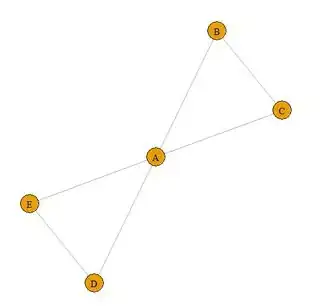
In this case, We can still assign a HouseID to each edge, even though the node A is in two different Houses. Notice that the edge A-B has HouseID = 2, but edge D-A has HouseD = 1. The HouseID is a property of the edge, not the node.

However, there is still a problem. It is possible for both ends of an edge to belong to two houses and one cannot assign a single house to the edge.

Edges4 = read.table(text="ID.1    ID.2
 A       B 
 A       C
 B       C
 D       A
 D       B", 
header=TRUE, stringsAsFactors=FALSE)

g4 = graph_from_edgelist(as.matrix(Edges4), directed=FALSE)
plot(g4)
MC4 = max_cliques(g4)
MC4
[[1]]
+ 3/4 vertices, named, from fbd5929:
[1] A B C

[[2]]
+ 3/4 vertices, named, from fbd5929:
[1] A B D

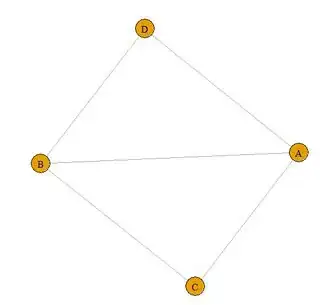
The edge A-B belongs to two maximal cliques. As @Scarabee said, the question is not actually well-defined for all graphs.

answered Aug 12 '17 at 06:59

G5W

36,531
10
47
80

thanks for the explanation . After Scarabee pointed out - i looked into graph theory to understand it. Broad problem to give you an idea is to - understand from a data engineering standpoint that - given the address , emails and Policy relation ( Insurance ) first identify linkages or relations - This i have already populated i.e. the edges ( so called relations of A and B ), Now task was how to identify households in my customer data base. This answer gives me a good starting point , however if there is a better methodology that you can suggest , do share. – Learner_seeker Aug 13 '17 at 04:33
i wanted to define two things - Household ( All relations of edges at first level - A to B , B to C , A to C , A to D . Other thing was community which captured all relations including indirect relations . Ex A is related to B , B is related to C , hence A and C might know each other. Hence rather than calling it one house - i call it a community. This community by definition will have multiple houses. Purpose was to cater for scenarios like If A ( Father ) related to B ( daughter ) , B is related to C ( Husband ) which is now a different house and hence should not be clubbed as one – Learner_seeker Aug 13 '17 at 04:36
@Pb89 So examples where a node is in two houses certainly could happen (e.g. shared custody of a child after parents divorce and remarry), but for your problem, shared edges do not seem very likely.. – G5W Aug 13 '17 at 11:15
The code you provided is going on a long run at `max_cliques(g4)` and after hours still hasn't finished - not sure if a desktop R will be able to handle it ? my data is huge with about 800k edges - would it be because of that ? – Learner_seeker Aug 15 '17 at 01:06
Yes. [Wikipedia](https://en.wikipedia.org/wiki/Clique_problem) says that to find all maximal cliques has a worst-case complexity of `O(3^(n/3))` where n is the number of nodes. The `apply` - `sapply` part should be fast, but maximal cliques will be expensive if you have a lot of nodes. – G5W Aug 15 '17 at 12:37
i ran the code as shared. I am getting Same no of IDs as edges - i.e. it is not forming ids for a network as the case above but assigning each row( edges) an ID – Learner_seeker Aug 22 '17 at 10:28
It is not identifying maximum cliques properly . It is identifying A to B and A to C as separate and with 2 cliques and giving 2 IDs , is it some simple data format issue ? I am using in same format as shared by you above – Learner_seeker Aug 22 '17 at 10:36
@Pb89 Yes. Your original question assigned IDs to _pairs_ of points, ie edges. This code will do that too. Thus, a single node might be in several cliques. That is part of the point of the extra examples. What would you want the answer to be for the first picture above - the one with 5 nodes? – G5W Aug 22 '17 at 11:58
It should come under one house ID - for the picture with 5 nodes. But irrespective , shouldn't a simple A to B and A to C , have a same house ID as per your code ? While i can plot and see the edges but its reflecting in the House IDs where each edge is getting its own ID – Learner_seeker Aug 22 '17 at 14:18
@Pb89 Just to clarify, I don't think that each _edge_ is getting a different HouseID, but rather each _clique_ is getting a HouseID. (That does mean that some nodes will be in two houses). - - - I think that you answered that for the picture with 5 nodes, you want only one HouseID. So you want B & E in the same House even though there is no direct connection between them? Is that correct? – G5W Aug 22 '17 at 14:46
Yes correct. I'll consider the indirect linkage between B and E in the same house ID. However like i pointed earlier - for some reason i am not getting house Id for _cliques_ but for each edge . So if my table has 25 edges for example , i am getting 25 IDs - using the same code as above. Not sure if its a data format related issue or something else ? Any alternative code suggested ? - Key thing is to generate the IDs – Learner_seeker Aug 22 '17 at 14:58
You see that on the original data that you provided, I got two IDs for 12 nodes. Are you getting that as well? It is only on your real data that it does not work? Or is it also giving 1 ID per edge on the sample data? – G5W Aug 22 '17 at 15:25
Let us [continue this discussion in chat](http://chat.stackoverflow.com/rooms/152548/discussion-between-pb89-and-g5w). – Learner_seeker Aug 22 '17 at 16:00

Detect Networks/communities and assign IDs

1 Answers1